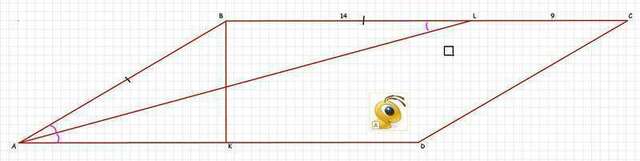
Дано: ABCD - параллелограмм;
угол А=30;
AL - биссектриса угла;
BL=14, LC=9
Найти: S=?
Решение.
Сторона параллелограмма AD=ВС=BL+LC=14+9=23.
Значит, треугольник ABL - равнобедренный, откуда имеем: АВ=ВL=14
Проведём высоту параллелограмма ВК.
Рассмотрим треугольник АВК. Поскольку катет, лежащий против угла в 30 градусов, равен половине гипотенузы, то ВК=1/2 * АВ=1/2 * 14=7
Площадь параллелограмма равна произведению стороны на высоту, опущенную на эту сторону:
S=AD*BK=23*7=161
Ответ: Площадь параллелограмма 161 кв.см