СРОЧНО ПОМОГИТЕ РЕШИТЬ 2 ПРИМЕРА! Задание сложное и мне нужно очень подробное решение!...

Question

24 просмотров

СРОЧНО ПОМОГИТЕ РЕШИТЬ 2 ПРИМЕРА! Задание сложное и мне нужно очень подробное решение! Поэтому даю много баллов за задание!!! По возможности, сфотографируйте решение и выложите картинками, буду очень признателен!!!!!

Задание: Провести ПОЛНОЕ ИССЛЕДОВАНИЕ и построить ГРАФИК ФУНКЦИИ.

Делать по вот этим пунктам:
1. область определения
2.четная или нечетная
3. периодичность
4.пересечение с осями
5.знаки функции
6.асимптоты
7.монотонность (точки минимума и максимума)
8.выпуклость
И потом после всех пунктов график!

Нужно решить оба примера пример, в идеале решённые!!!

Алгебра ОлВиКо_zn (125 баллов) 07 Май, 18 | 24 просмотров

Дан 1 ответ

Правильный ответ

$y=2x^3+3x^2-5$

1. Найдем область определения функции. Т. к. в уравнении функции отсутствует деление на переменную, извлечения корней, отрицательные или нецелые показатели степени, логарифмы, тангенсы, арккосинусы и арксинусы, то мы вправе заявить, что областью определения данной функции является вся числовая прямая. [-∞;+∞]

2. Т.к. границ области определения нет, то следовательно у функции нет и вертикальных асимптот.

3. Исследование функции на четность и нечетность.
Функция является четной, если выполняется равенство $y(-x)=y(x)$ Четность функции указывает на симметричность графика относительно оси ординат (оY). Нечетность функции обуславливается выполнением равенства $y(-x)=-y(x)$ и указывает на симметричность графика относительно начала координат. Если же ни одно из равенств не выполняется, то перед нами функция общего вида.
В нашем случае выполняется ни одно равенство не выполняется следовательно наша функция общего вида.

4. Находим промежутки возрастания и убывания функции и точки экстремума. Находим производную функции на области определения
$(2x^3+3x^2-5)'=2*3x^2+3*2x=6x^2+6x$
находи стационарные точки $6x^2+6x=0 \\ 6x(x+1)=0 \\ x_1=0 \\ x_2=-1$
наносим точки на числовую прямую и определяем знак производной внутри промежутка
$f'(-2)=6*(-2)^2+6*(-2)=6*4-62=24-12=12\ \textgreater \ 0 \\ f'(-0.5)=6*(-0.5)^2+6*(-0.5)=6*0.25-3=1.5-3=-1.5\ \textless \ 0 \\ f'(1)=6*1^2+6*1=6+6=12\ \textgreater \ 0$

___+___-1____-_____0______+______
возраст. убывает возраст.

точками экстремума являются точки в которых функция определена и проходя через которые она меняет свой знак.

5. Находим промежутки выпуклости и вогнутости и точки перегиба функции.
находим вторую производную $(6x^2+6x)'=6*2x+6$
находим нули второй производной $12x+6=0 \\ 12x=-6 \\ x=-0,5$
наносим точку на числовую прямую и определяем знак второй производной внутри промежутка
$f"(-2)=12*(-2)+6=-24+6=-18\ \textless \ 0 \\ f"(0)=12*0+6=6\ \textgreater \ 0$

____-____-0,5_____+_______
выпукл. вогнут.

точка -0,5 является точкой перегиба, т.к. вторая производная меняет знак проходя через нее, в самой точке вторая производная равна нулю и точка принадлежит области определения функции.

6. Нахождение горизонтальных и наклонных асимптот. Горизонтальные и наклонные асимптоты следует искать только тогда , когда функция определена на бесконечности. Они очень помогают при построении графика. Наклонные асимптоты ищутся в виде прямых вида $y=kx+b \\ k= \lim_{x \to \infty} \frac{f(x)}{x} \\ \\ b= \lim_{x \to \infty} (f(x)-kx)$

7. Находим пересечение функции осями. С осью абцисс
$2x^3+3x^2-5=0$ x=1
с осью ординат $6*0^3+6*0^2-5=0+0-5=-5$

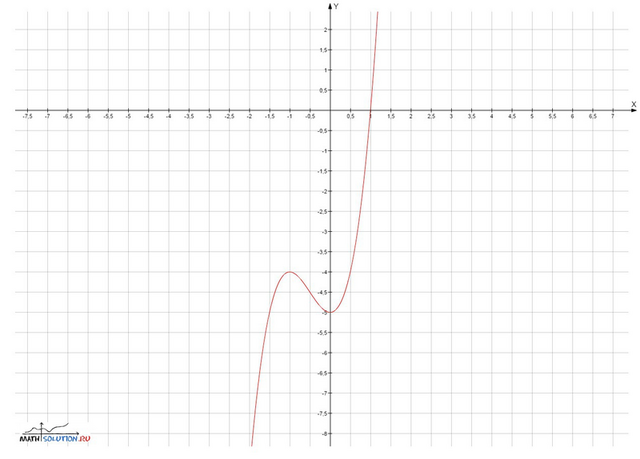
8. строим график

CVita_zn (54.8k баллов) 07 Май, 18