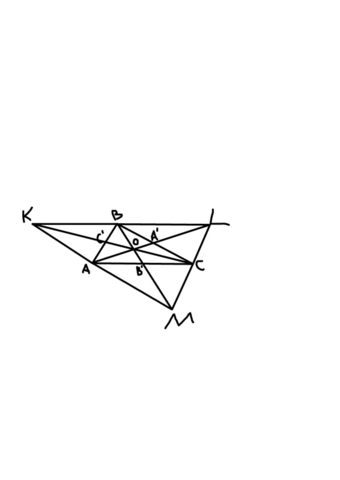
Пусть тр-к ABC имеет медианы AA', BB', CC', построим около него тр-к KLM такой, что KAB подобен CBA, LCB подобен ABC, MAC подобен BCA.
Такое постороение возможно, потому что тогда угол CBL + угол ABK + B = 180 так как CBL = C, ABK = A; A + B + C = 180. Аналогично с остальными сторонами.
Так как АВС подобен трем другим тр-кам, то получилось 3 параллелограмма: ABLC, ABCM, AKBC
Как известно, в параллелограмме сумма квадратов сторон равна сумме квадратов диагоналей. Тогда BC^2 + AL^2 = 2AB^2+2AC^2 => AL^2=2AB^2+2AC^2-BC^2


Аналогично с остальными медианами - медиана равна половине корня из суммы удвоенных квадратов сторон, образующих угол, из которого опускается медиана, без квадрата стороны, на которую она опущена