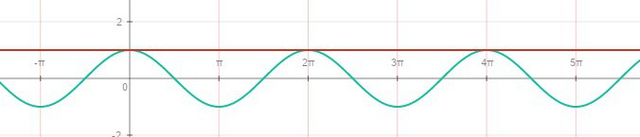
Cos α=1;
α=2πn, n∈Z.
Теперь найдем корни уравнения, принадлежащие промежутку [-π;5π].
Это можно сделать алгебраическим способом с помощью неравенства:
-π≤2πn≤5π;
Сокращаем на π, получаем:
-1≤2n≤5;
Теперь делим на 2:
-1/2≤n≤2,5.
Т.е. целые значения n=0; 1; 2.
Значит, корня будет три. Найдем их:
При n=0 α1=2π*0=0;
При n=1 α2=2π*1=2π;
При n=2 α3=2π*2=4π.
Эти решения хорошо видны и на графике.