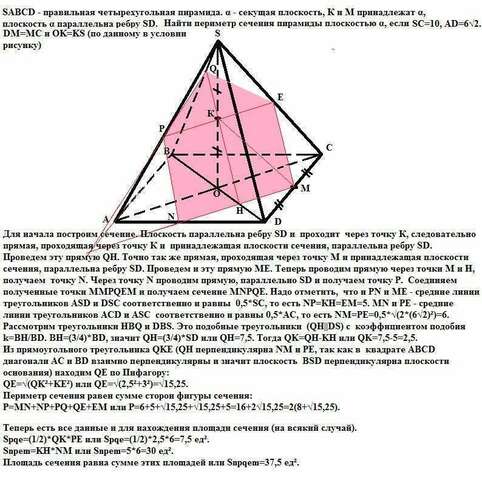
Для начала построим сечение. Плоскость параллельна ребру SD и проходит
через точку К, следовательно прямая, проходящая через точку К и
принадлежащая плоскости сечения, параллельна ребру SD.
Проведем эту прямую QH. Точно так же прямая, проходящая через точку М и принадлежащая плоскости сечения, параллельна ребру SD.
Проведем
и эту прямую МЕ. Теперь проводим прямую через точки М и Н, получаем
точку N. Через точку N проводим прямую, параллельно SD и получаем точку
Р. Соединяем полученные точки МMPQEM и получаем сечение MNPQE. Надо
отметить, что и PN и МЕ - средние линии треугольников ASD и DSC
соответственно и равны 0,5*SC, то есть NP=КН=ЕМ=5.
MN и PE - средние линии треугольников AСD и АSC соответственно и равны 0,5*АC, то есть NМ=РЕ=0,5*√(2*(6√2)²)=6.
Рассмотрим треугольники НВQ и DBS. Это подобные треугольники (QH||DS) с
коэффициентом подобия k=BH/BD. ВН=(3/4)*BD, значит QH=(3/4)*SD или QH=7,5. Тогда QK=QH-KH или QK=7,5-5=2,5.
Из прямоугольного треугольника QKE (QH перпендикулярна NM и РЕ, так как в
квадрате
АВСD диагонали АС и ВD взаимно перпендикулярны и значит плоскость ВSD
перпендикулярна плоскости основания) находим QE по Пифагору:
QE=√(QK²+KE²) или QE=√(2,5²+3²)=√15,25.
Периметр сечения равен сумме сторон фигуры сечения:
Р=MN+NP+PQ+QE+EM или Р=6+5+√15,25+√15,25+5=16+2√15,25=2(8+√15,25).
P.S Теперь есть все данные и для нахождения площади сечения (на всякий случай).
Spqe=(1/2)*QK*PE или Spqe=(1/2)*2,5*6=7,5 ед².
Snpem=KH*NM или Snpem=5*6=30 ед².
Площадь сечения равна сумме этих площадей или Snpqem=37,5 ед².