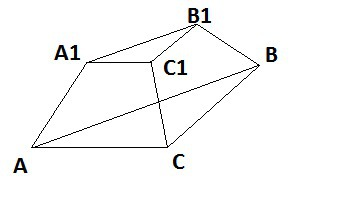
Пусть ABCA1B1C1 - усечённая пирамида. Треугольники ABC и A1B1C1 - прямоугольные, с прямыми углами C и C1 соответственно. Углы B и B1 равны 60 градусов. Высота пирамиды (нарисуйте сами) равна √3. AB = 6, A1B1 = 4.
Для определения объёма пирамиды нам нужно знать её высоту и площади оснований. Для этого нам необходимо найти катеты треугольников ABC и A1B1C1
Из треугольника ABC
1) по определению синуса
sinB = AC/AB
AC = AB*sinB = 6*√3/2 = 3√3
2) по определению косинуса
cosB = BC/AB
BC = AB*cosB = 6*1/2 = 3
Аналогично находим катеты треугольника A1B1C1:
A1C1 = A1B1*sinB1 = 4*√3/2 = 2√3
B1C1 = A1B1*cosB1 = 4*1/2 = 2
Найдём площади оснований:
S(ABC) = AC*BC/2 = 3*3√3/2 = 9√3/2
S(A1B1C1) = A1C1*B1C1/2 = 2*2√3/2 = 2√3
Тогда объём усечённой пирамиды
V = 1/3*h*(S1+S2+√(S1S2)) = √3/3*(9√3/2+2√3+√(9√3/2*2√3)) = √3/3*(9√3/2+4√3/2+√(18*3/2)) = √3/3*(13√3/2+√27) = √3/3*(13√3/2+3√3) = √3/3*(13√3/2+6√3/2) = √3/3*19√3/2 = (3*19)/(3*2) = 19/2 = 9,5