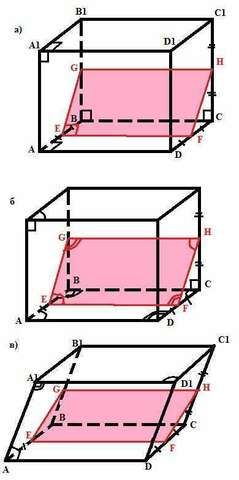
Поскольку сечение проходит через середины ребер АВ и СD, линия пересечения секущей плоскости и основания параллельна и равна стороне АD.
А так как сечение проходит через середину ребра ВВ1, линия пересечения секущей плоскости и боковой грани ВВ1С1С параллелепипеда так же параллельна и равна стороне АD.
Значит в общем случае сечение имеет вид параллелограмма, так как если две противоположные стороны четырехугольника равны и параллельны, то этот четырехугольник - параллелограмм.
Тогда вид сечения в случае
а) прямоугольного параллелепипеда - прямоугольник, так как углы ВAD и СDA параллелепипеда прямые, значит и соответственные углы сечения GЕF и HFE также прямые.
б) прямого параллелепипеда - параллелограмм, так как в основании такого параллелепипеда лежит параллелограмм и углы ВAD и СDA не прямые.
в) в случае наклонного параллелепипеда - так же параллелограмм, так как и в этом случае в сечении нет прямых углов.