Решите пожалуйста №23 с подробным решением,что и как находилось.За ранее спасибо)!

Question

Дан 1 ответ

Правильный ответ

$y= \frac{x^4-13x^2+36}{(x-3)(x+2)}$

ОДЗ:

$x-3\neq0\\ \boxed{x\neq3}\\\\ x+2=0\\ \boxed{x\neq-2}$

$D(f)=(-\infty;-2)\bigcup(-2;3)\bigcup(3;+\infty)$

$y= \frac{x^4-13x^2+36}{(x-3)(x+2)} = \frac{(x-2)(x+2)(x-3)(x+3)}{(x-3)(x+2)}=(x-2)(x+3)=x^2+x-6$

$\boxed{*}\\ x^4-13x^2+36=0\\ x^2=t\\ t^2-13t+36=0\\ D=169-144=25; \sqrt D= 5\\\\ t_{1/2}= \frac{13\pm5}{2}\\\\ t_1= \frac{8}{2}=4\\\\ t_2= \frac{18}{2}=9$

Обратная замена:

$x^2=4\\ x_{1/2}=\pm2\\\\ x^2=9\\ x_{1/2}=\pm3$

$x^4-13x^2+36=(x+2)(x-2)(x-3)(x+3)$

Приступим к построению функции $y=x^2+x-6=0$

Корни у нас уже известны (как видно из упрощения функции), соответственно:

$x^2+x-6=(x-2)(x+3)$

$x-2=0\\ x=2\\\\ x+3=0\\ x=-3$

Находим координату вершины параболы $(x_0;y_0)$

$x_0= -\frac{b}{2a}= -\frac{1}{2}$

Чтобы найти $y_0$ необходимо значение $x_0$ подставить в нашу функцию, получаем:

$y_0=(- \frac{1}{2})^2- \frac{1}{2}-6= \frac{1}{4}- \frac{1}{2}-6= \frac{1-2-24}{4}=- \frac{25}{4}=-6.25$

ОДЗ нам показывает точки, в которых функция не может существовать, т.е. она прерывается. Подставим значения ОДЗ в уже упрощенную функцию:

$y(-2)=(-2-2)(-2+3)=-4\cdot1=-4\\ y(3)=(3-2)(3+3)=1\cdot6=6$

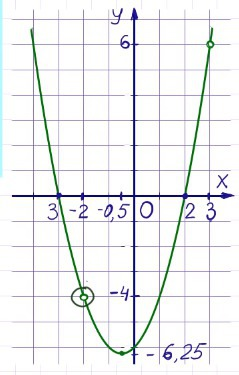
Обозначаем эти точки на графике (см. график)

Переходим к определению, при каких значениях с прямая у=с имеет с графиком одну общую точку.

Понимаем, что прямая у=с - это прямая, параллельная оси ОХ. Мы должны найти такие значения этой прямой, чтобы график она пересекала в одной точке.
Первая точка - это вершина параболы, в ней прямая будет иметь одну точку соприкосновения. с = -6,25

Вторая точка - это выколотая точка у(-2) = -4. Слева прямая пройдет через разрыв функции, а правую ветвь пересечет. с=-4

Третья точка - это выколотая точка у(3) = 6. Слева прямая пересечет график, а справа пересечения не будет. с=6

Итак, мы нашли три точки пересечения графика с прямой, где прямая будет иметь с графиком три общие точки.

Ответ: $c_1=-6.25; \ c_2=-4; \ c_3=6$

eugeke_zn (29.3k баллов) 08 Май, 18