Произвести полное исследование функции и построить график. (УСЛОВИЕ ** КАРТИНКЕ) План: 1)...

Question

Произвести полное исследование функции и построить график. (УСЛОВИЕ НА КАРТИНКЕ)
План:
1) Найти область определения функции.
2) Исследовать функцию на четность и нечетность
3) Исследовать на периодичность
4)Исследовать на непрерывность, найти точки разрыва.
5)Найти критические точки первого рода
6) Найти интервалы монотонности и экстремумы функции
7)Найти критические точки второго рода
8) Найти интервалы выпуклости и точки перегиба
9) Найти асимтоты графика функции
10) Найти точки пересечения графика с осями
11) Построить график

---

Answer 1

ДАНО
Y=ln(x²-4x+8)
ИССЛЕДОВАНИЕ
1.Область определения  X∈(-∞,+∞)
2. Пересечение с осью абсцисс - ось Х - корней нет.  
3. Пересечение с осью ординат - ось У - Y(0) = ln(8)
4. Поведение на бесконечности
Y(-∞) = +∞,  Y(+∞) = +∞
5. Исследование на четность
Y(x) = ln(x²-4x+8)
Y(-x) = ln(x²+4x+8)
Функция ни чётная ни нечётная.
6. Производная функции
Y' = (2x-4)/(x²-4x+8)
7. Нули производной
Х=2 - минимум  Ymin(2) = ln4
8.
Убывает - Х∈(-∞,2]
Возрастает - X∈[2,+∞)
9. Вторая производная.

10. Корни второй производной -  х1 - 0 и х2 = 4.
Вогнутая - "ложка" - Х∈[0,4]
Выпуклая - "горка" - X∈(-∞,0]∪[4,+∞).
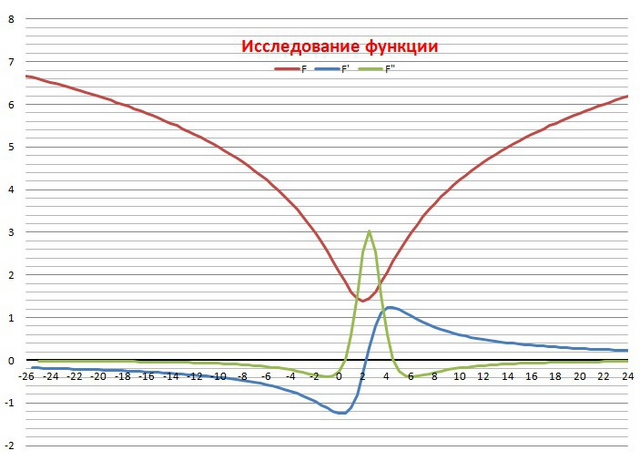
11. График прилагается вместе с графиками производной.

---

Comments

Вогнутость, наверно, не правильно. Точки перегиба есть.

---

ДОПОЛНЕНО