1) Найдите область определения: y=lg(-2+x+x^2) 2) Сравните числа log 3,07 по основанию...

Question

1) Найдите область определения: y=lg(-2+x+x^2)
2) Сравните числа log 3,07 по основанию 3/5 и log 3,7 по основанию 3/5
3) Решить графически log x по основанию 1/2 < (1/2)x -2

Comments

помогите http://znanija.com/task/21067542

Answer 1

1) y = lg(x^2+x-2)
x^2+x-2 > 0
• x^2+x-2 = 0
• D = 1^2-4×1×(-2) = 1+8 = 9 D^(1/2) = 3
• x[1] = (-1-3)/2 = -2
• x[2] = (-1+3)/2 = 1
D(f) = (-∞;-2)U(1;+∞)

2) log[3/5](3,07); log[3/5](3,7)
log[3/5](3,07) ≈ -2,2
log[3/5](3.7) ≈ -2,6
-2,2 > -2,6
log[3/5](3,07) > log[3/5](3,7)

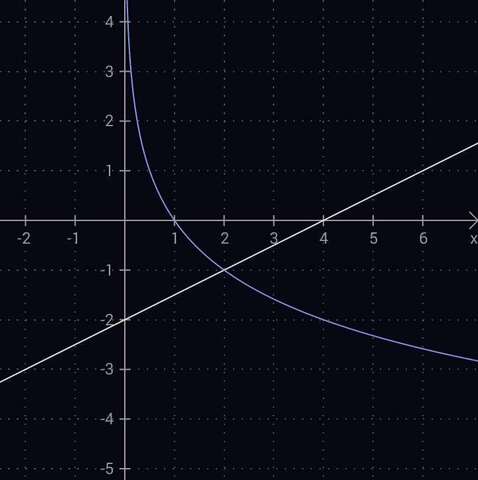
3) log[1/2](x) < (1/2)x-2
y = log[1/2](x)
y = (1/2)x-2
x = 2

---