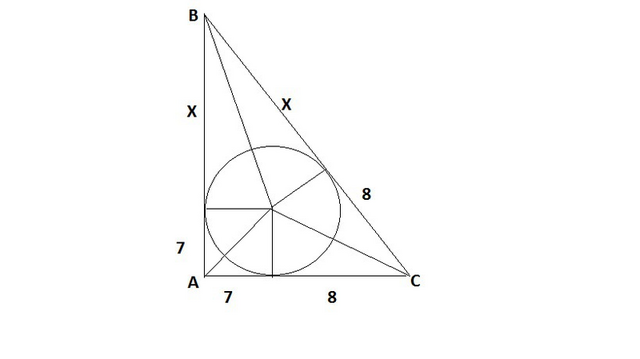
Диаметр окружности описанной около прямоугольного треугольника равен его гипотенузе.
Если из точки, лежащей вне окружности, провести касательные, то расстояния от точки до точек касания равны.
Далее по т. Пифагора находим Х:
(7+х)² + 15²=(8+х)²
49+14х+х²+225=64+16х+х²
2х=210
х=105;
гипотенуза - диаметр описанной окружности - х+8=105+8=113 см.