Две медианы равнобедренного треугольника взаимно перпендикулярны. Боковая сторона равна...

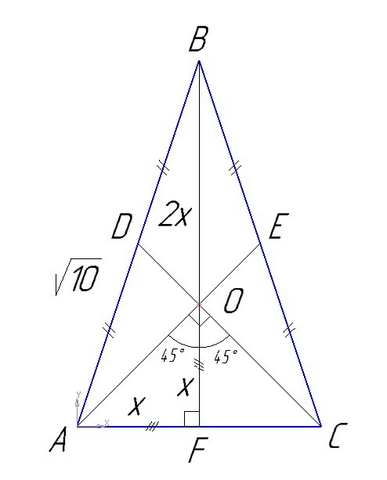
Решение.

Из условия задачи АВ = ВС, ΔАВС - равнобедренный, тогда медианы AE=СD.
В равнобедренном треугольнике высота BF является и медианой, и биссектрисой. Т.к. точка О - точка пересечения медиан, через которую проходит и BF, то ∠АОС делится пополам. По условию задачи медианы взаимно-перпендикулярны, тогда
∠ АOF = ∠FOC = ∠AOC / 2 = 90° / 2 = 45°
Учитывая, что ∠AFB = 90°, a ∠AOF = 45° ⇒ ∠OAF = 45° , тогда ΔAOF - равнобедренный, т.е. AF = OF

Пусть AF = x, OF = x, BO = 2x, BF = 3x
ΔAFB - прямоугольный, тогда по теореме Пифагора
АВ² = AF² + BF²

$( \sqrt{10} )^2 = x^{2} + (3x)^2 \\ \\ 10 x^{2} = 10 \\ \\ x=1$

Значит АС = 2AF = 2 *1 = 2, BF = 3 * 1 = 3

Найдем площадь
$S_{ABC} = \frac{1}{2}AC*BF = \frac{1}{2}*2 * 3 = 3$ кв.ед.

Ответе: S = 3 кв.ед.