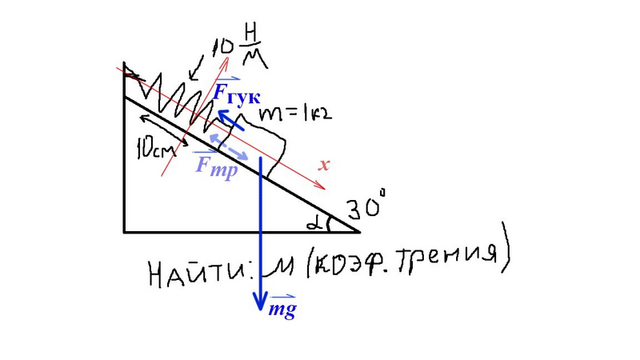
Введём систему координат Оху так, чтобы ось Оу была направлена вверх поперёк (!) наклонной плоскости, а ось Ох вниз вдоль (!) наклонной плоскости. При этом за нулевую точку примем правое окончание пружины. Тогда положительная координата x – будет как раз означать растяжение пружины, а отрицательная координата x – будет означать сжатие пружины.
Сила трения направлена вдоль наклонной плоскости, поэтому её проекция на ось Оу равна нулю, а проекция на ось Ох по модулю равна самой силе трения. При этом в разных состояниях движения – сила трения может быть направлена в разные стороны, т.е. проекция может иметь как знак плюс, так и знак минус. А в различных состояниях покоя – сила трения покоя не только может иметь разные направления, но и не равна по модулю силе трения покоя Fтр≠μN, а меньше неё, т.е. Fтр<μN, т.е. |Fтрx|<μN .<br>
Поставленные условия не уточняются обстоятельствами, при которых система пришла в равновесие. И можно предположить, как минимум, четыре разных способа достижения равновесия:
Подзадача-1: Груз после подвешивания просто отпустили. При этом система начинает совершать квазигармонические затухающие колебания в условиях сухого трения, которые описываются стандартной гармонической функцией косинуса с ненулевым постоянным по модулю уровнем равновесия, знак которого переключается на каждом новом полупериоде (отсчитывая от начального момента времени). Эта задача наиболее трудна для решения при строгом обосновании всех факторов.
Подзадача-2: Груз после подвешивания не отпускают, а подпирая снизу (с правого торца), очень медленно (квази-статично) позволяют ему сползать по плоскости за счёт превалирующей силы тяжести, не допуская разгона и не помогая ему. При этом очевидным следствием достигнутого устойчивого равновесия является его «пограничность», т.е. если мы хотя бы на миллиметр подвинем груз вдоль плоскости вверх – он снова начнёт сползать обратно вниз вдоль неё. В этом случае, ясно, что в любой момент времени – сила трения будет направлена против сползания, т.е. строго вверх вдоль (!) наклонной плоскости. При этом, поскольку до последнего момента установления равновесия груз двигается (!), то значит, сила трения всегда равна именно силе трения скольжения, т.е. Fтр=μN, т.е. Fтрх=–μN . Такую задачу решить проще всего.
Подзадача-3: Груз после подвешивания не отпускают, а тянут вниз, растягивая пружину до такого состояния, чтобы груз начал двигаться обратно вверх. При этом грузу не дают двигаться свободно обратно вверх, а подпирая сверху (со стороны крепления к пружине!), очень медленно (квази-статично) позволяют ему заползать вверх по плоскости за счёт превалирующей возвратной силы Гука (упругости), не допуская разгона и не помогая ему. При этом очевидным следствием достигнутого устойчивого равновесия является его «пограничность», т.е. если мы хотя бы на миллиметр подвинем груз вдоль плоскости вниз (!) – он снова начнёт заползать обратно вверх вдоль неё. В этом случае, ясно, что в любой момент времени – сила трения будет направлена против «заползания», т.е. строго вниз вдоль (!) наклонной плоскости. При этом, поскольку до последнего момента установления равновесия груз двигается (!), то значит, сила трения всегда равна именно силе трения скольжения, т.е. Fтр=μN, т.е. Fтрх=μN . Эту задачу тоже решить несложно.
Подзадача-4: Груз после подвешивания не отпускают, а некоторым случайным образом растягивая пружину, кладут его в новое положение, и оказывается, что в этом положении груз находится в состоянии устойчивого равновесия. Причём в этом случае, медленный сдвиг на небольшие расстояния вдоль плоскости вверх и вниз – не приведёт груз в движение, т.е. такое равновесие не только устойчивое, а ещё и безразлично-устойчивое. Как именно при этом будет направлена сила трения покоя – неизвестно, поэтому для такой подзадачи нужно рассматривать силу трения в общем случае, и её нельзя считать просто равной силе трения скольжения, т.е. Fтр≠μN, а |Fтрх|<μN или –μN < Fтрх <μN . Эту задачу решать – чуть сложнее. Она фактически объединяет в себе подзадачи 2 и 3, и её решение уже будет представлять собой не решение уравнения, а решение неравенства.<br>
*** Инвертированная задача: Если бы в задаче были даны жёсткость, масса, угол наклона и трение, а спрашивалось бы о величине возможного отклонения от положения равновесия (т.е. величине растягивания пружины), то тогда ответом на такую задачу было бы не конкретное значение отклонения, а диапазон, как при решении любого математического неравенства. Эта задача чуть похожа на подзадачу-4, и решить её – даже проще.
Решения поставленных задач – в добавленном документе.
Подзадача-1. Ответ: μ ≈ 0.52 ;
Подзадача-2. Ответ: μ ≈ 0.46 ;
Подзадача-3 c данными значениями остальных величин не имеет смысла.
Подзадача-4. Ответ: μ > 0.46 .
*** Инвертированная задача со значением μ ≈ 0.46. Ответ: 10 см < x < 88 см.
Скачать вложение Adobe Acrobat (PDF)