Длина гипотенузы равнобедренного прямоугольного треугольника равна 40. Окружность радиуса...

Question

Длина гипотенузы равнобедренного прямоугольного треугольника равна 40. Окружность радиуса 9 касается гипотенузы в ее середине.Найти длину отрезка, отсекаемого этой окружностью на одном из катетов.

Answer 1

Не буду рисовать рисунок ! так как у предыдущего ответа есть рисунок я буду по ней решать!
треугольник равнобедренный , по свойству касательной проведенной с одной точки 
OB касательная к окружности, стало быть ВЕ секущая  , по формуле 
OB^2=BK*BE =BK(EK+KB)
СО тоже секущая и она же высота равнобедренного треугольника , по свойству 
CE*EK=CL*LE  (точка L это точка где окружность пересекает  высоту)
у нас известно что ОВ это середина значит 40/2=20
Найдем катет треугольника так как у нас треугольник равнобедренный то 
2BC^2=40^2
BC=20√2
Теперь найдем высоту треугольника  H=√(20√2)^2-20^2 = 20 
и найдем отрезок CL=20-2R = 2см

Ставим все в наше уравнение
400=BK(EK+KB)
40=(CE+EK)*CE
СЕ+EK+BK=20√2

решаем систему! 
сделаем замену чтобы удобней решалось 
BK=x
EK=y
CE=z

400=x(y+x)
40=y*(z+y)
x+y+z=20√2

выразим y+z  третьего уравнения 
y+z=20√2-x

40=y*(20√2-x)
400=x(y+x)

40=20√2y-yx
400=yx+x^2


40=20√2y-(400-x^2)
440=20√2y+x^2
y=440-x^2/20√2 

получаем x =-√82-29√2/2   y=√82 =EK  Ответ   √82

Comments

Вы обратите внимание, каким техническим приемом я решил ту систему, которую Вы делали. Это у меня в комментарии. Тут тот случай, когда прием решения на много ценнее самой системы.

---

я так для разнообразия решил

---

да я понял, я тоже сначала сделал в лоб, как Вы. Просто тут техническая сложность системы зависит от удачного выбора неизвестных. В данном случае, вместо СЕ, ЕК и КВ можно сразу выбрать ЕК и СQ и QB, где Q - середина EK. Тогда система почти устная получается.

---

когда такие системы , думать как бы схитрить как то неохота , уже охота найти просто значение переменных

---

У меня визуальное мышление :) поэтому я всегда ищу способы решения, не требующие сложных вычислений, а точнее - когда пространственные связи компенсируют значительную часть сложностей. Это примерно, как сборка кубика Рубика. Просто собрать его может любой, кто знает "методы". Но правильное комбинирование некоммутирующих операций позволяет собирать его за секунды. :)

Answer 2

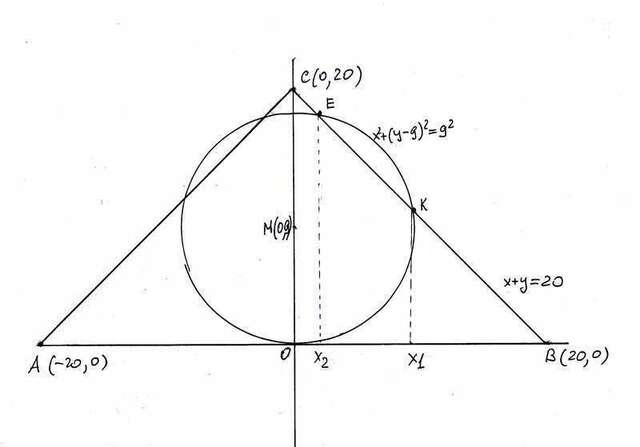
Если поместить центр начала координат в середину гипотенузы и провести ось Y через вершину прямого угла, а ось X вдоль гипотенузы, то вершины треугольника будут иметь координаты (20,0) (-20,0) (0,20), а центр окружности радиуса 9 будет находиться в точке (0, 9). Уравнение стороны и уравнение окружности выглядят так.
x + y = 20;
x^2 + (y - 9)^2 = 9^2;
отсюда y - 9 = 11 - x; и для точек пересечения получается квадратное уравнение на их координаты x1 и x2; 
x^2 + (11 - x)^2 = 9^2; или x^2 - 11*x + 20 = 0;
x1 = (11 + √41)/2; x2 = (11 - √41)/2; 
Расстояние между точками пересечения стороны и окружности, очевидно, равно
d = (x1 - x2)*√2 = √82;

---

Comments

Это длина хорды, то есть части стороны ВНУТРИ окружности. Там есть еще два отрезка стороны снаружи, длины их легко найти из решения.

---

Я что-то не могу сообразить...может быть не хватает рисунка.

---

здесь метод координат самый разумный

---

А я таки решил правильно без метода координат. Если КВ = n; EK = m; CE = p; то (n+m)*n = 400; (p+m)*p = 20*(20-18) = 40; n + m+p = 20√2; это верная система, и она решается легко. Самое простое - пусть t = n + m/2; u = p + m/2; тогда t^2 - (m/2)^2 = 400; u^2 - (m/2)^2 = 40; t + u = 20√2; => t^2 - u^2 = 360; t - u = 360/(20√2) = 9√2; t = 29√2/2; (m/2)^2 = t^2 - 400 = 41/2; m = √82;

---

я только что решил

---

ну так добавьте ответ, вместо удаленного :)

---

добавил

---

все равно методом координат удобней

---

это да, согласен :) в данном случае координатным методом задачка решается сама собой, без усилий мозга.