Из комментариев условие задачи выглядит так:
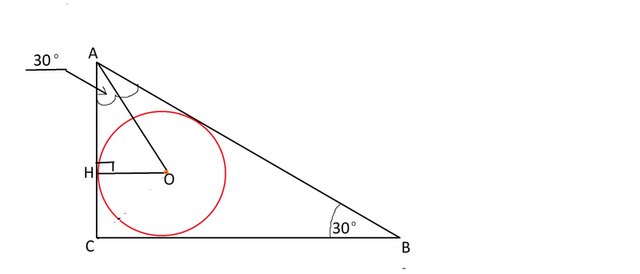
В прямоугольном треугольники АВС угол В 30°, угол С 90°, О - центр вписанной окружности. Отрезок ОА=12 . Определить радиус вписанной окружности.
---------------------------------
Так как угол В равен 30°, угол А равен 60°.
Центр вписанной окружности лежит на биссектрисе угла А.
АО - биссектриса.
Угол ОАН=30°.
ОН- радиус окружности и противолежит углу 30°.
ОН=АО*sin 30°=12*0,5=6 см
----
Если же, как дано первоначально в условии, АН=12 см , то
ОН=АН:tg 60°=12:√3=4√3r=4√3