1. Найдем выражение, формирующее числитель под знаком логарифма
Имеется ряд чисел 28, 47, 66, 95, ... 997.
Легко заметить, что этот ряд чисел - арифметическая прогрессия с разностью 47-28=19 и начальным членом a₀=28
Общий член такого ряда можно записать в виде
2. Найдем выражение, формирующее знаменатель под знаком логарифма
Имеется ряд чисел 14, 35, 56, 77, ... 1085.
И этот ряд чисел - тоже арифметическая прогрессия с разностью 35-14=21 и начальным членом b₀=14
Общий член такого ряда можно записать в виде
3. Как мы нашли, что общее количество членов ряда равно 52?
Для этого надо решить простейшее уравнение.
19n+9=997; 19n=989; n=989/19=52
Такой же результат даст решение и другого уравнения- 21n-7=1085, поэтому можно брать любое из них.
4. Мы видим, что вычисление надо начинать от последнего члена ряда и идти к первому, потому что нужно находить модуль от суммы текущего члена с последующим, а не с предыдущим. С этой целью перепишем наши порождающие формулы:
5. Теперь можно написать рекуррентную формулу для нахождения k-й частичной суммы:
![\displaystyle s_k:=\lg\left | \frac{1016-19k}{1106-21k}+s_{k+1}\right |, \quad k\in[1;52], \mathbb N](https://tex.z-dn.net/?f=%5Cdisplaystyle+s_k%3A%3D%5Clg%5Cleft+%7C+%5Cfrac%7B1016-19k%7D%7B1106-21k%7D%2Bs_%7Bk%2B1%7D%5Cright+%7C%2C+%5Cquad+k%5Cin%5B1%3B52%5D%2C+%5Cmathbb+N+ "\displaystyle s_k:=\lg\left | \frac{1016-19k}{1106-21k}+s_{k+1}\right |, \quad k\in[1;52], \mathbb N")
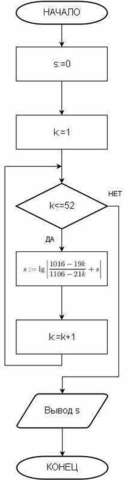
6. Само же вычисление несложно; блок-схема приведена во вложении.
