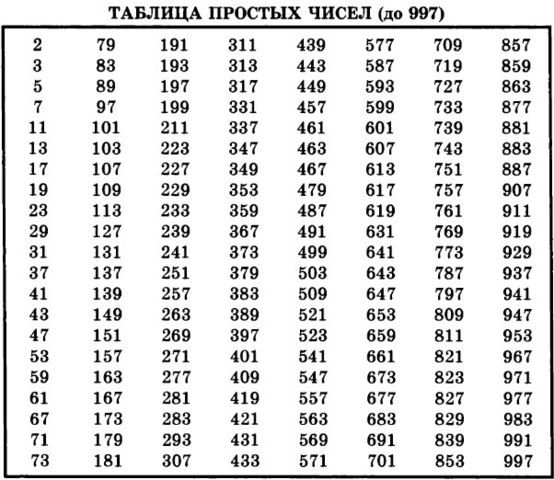
Один из множителей равен кубу, а минимальный куб который в произведении с трехзначным числом будет давать четырехзначное это 8. Значит нам нужно найти трехзначное простое число, сумма цифр в котором будет меньше 10 и которое будет в произведении с 8 давать четырехзначное число. Таких чисел всего 17:
131, 151, 211, 223, 233, 241, 251, 311, 313, 331, 401, 421, 431, 503, 521, 601, 701
Осталось только умножить каждое на 8 и проверить, чтоб сумма цифр трехзначного множителя соответствовала числу единиц в произведении. 251*8 = 2008 - число, которое соответствует условиям.
Если мы возьмем в качестве первого множителя следующий куб - 27, то произведение любого трехзначного числа на него будет больше 2008, то же касается куба 64. Значит 2008 - минимальное число, подходящее под условие
Ответ: 2008