ООФ то что под корнем ≥0 ⇒
х³-5х²+6х≥0
чтобы решить это неравенство разложим на множители левую часть
х(х²-5х+6)=х(х²-2х-3х+6)=х(х(х-2)-3(х-2))=х(х-2)(х-3)≥0
решим неравенство методом интервалов,
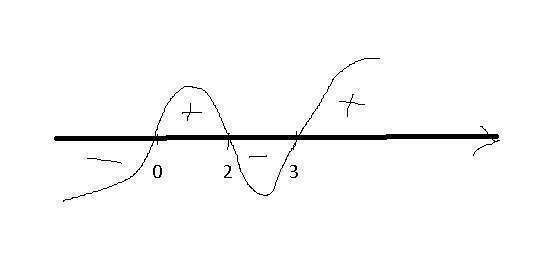
нанесем корни х={0;2;3} на числовую ось и определим знаки выражения х(х-2)(х-3) (1) на каждом из этих интервалов, для этого надо взять любое число из каждого интервала подставить вместо х в выражение 1 и посмотреть с каким знаком получится значение выражения если >0 то+ если <0 то -<br>например при х=10 10*(10-2)(10-3)=10*8*7=560>0 знак + , знаки на остальных интервалах можно не вычислять они будут чередоваться плюс с минусом так как функция у=х(х-2)(х-3) непрерывная см. картинку ,
выбираем те отрезки в которых значение выражения (1) ≥0 это и будет ООФ
х∈[0;2]∪[3;+∞)