Упростим:
x³+1=(x+1)·(x²-x+1)
x²-1=(x+1)·(x-1)
Таким образом:
f(x)=(x²-x+1)/(x-1)
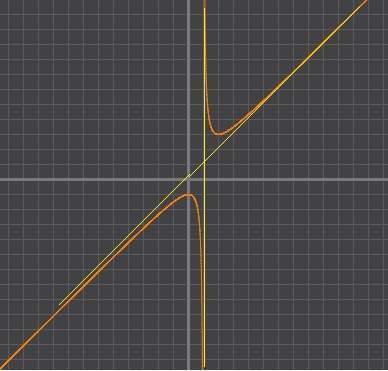
Вертикальная асимптота:
x=1
Наклонные асимптоты:
y=k*x+b
Находим предел при x →∞
k = lim f(x)/x = (x²-x+1) / (x*(x-1)) = 1
b = lim (f(x)-k*x)) = lim ((x²-x+1)/(x-1) - 1*x) =0
Наклонная асимптота
y=x
Схематично строим график: