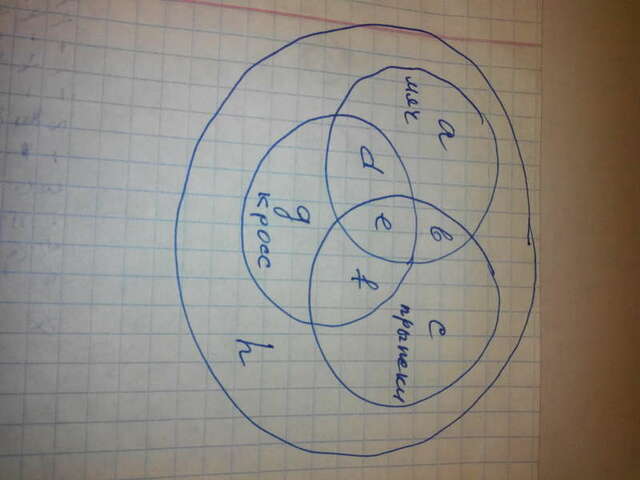
Эта задача решается при помощи кругов Эйлера (смотри рисунок)
- рисуем три пересекающихся круга по одному для каждого вида спорта. Те места, которые находят друг на друга - это учащиеся, которые приняли участие в нескольких видах спорта, а непересекающиеся участки - только в одном виде спорта.
внешний большой круг это всего учащихся 6-х классов, при чем та часть, которая не занята маленькими кругами, соответственно, не принимала участия в соревнованиях.
Обозначим все участки получившейся схемы буквами, как на рисунке и дальше решаем обычным арифметическим способом:
е=31
b+e=38 => b=38-31=7
f+e=42 => f=42-31=11
d+e=32 => d=32-31=1
a+b+d+e=50 => a=50-(7+1+31)=11
b+c+e+f=65 => c=65-(7+31+11)=16
d+e+f+g=48 => g=48-(1+31+11)=5
h+(a+b+c+d+e+f+g)=140 => h=140-(11+7+16+1+31+11+5)=58
Теперь, когда есть все данные, можем отвечать на вопросы задачи:
1) Сколько человек не участвовало в соревнованиях?
Это соответствует h.
Ответ: 58 человек не участвовало в соревнованиях
2) Сколько человек участвовало только в одном виде соревнований?
Это a+c+g=11+16+5=32
Ответ: 32 человека участвовало только в одном виде соревнований.
3) Сколько человек участвовало не менее чем в двух видах соревнований?
Это все кто участвовал в соревнованиях (140-h) минус те, кто участвовал только в одном виде соревнований (32):
140-h-32=140-58-32=50
Ответ: 50 человек участвовало не менее чем в двух видах соревнований.