Окружность, вписанная в ромб, точкой касании делит его сторону в отношении 2:3 Тогда...

Question

Дан 1 ответ

Правильный ответ

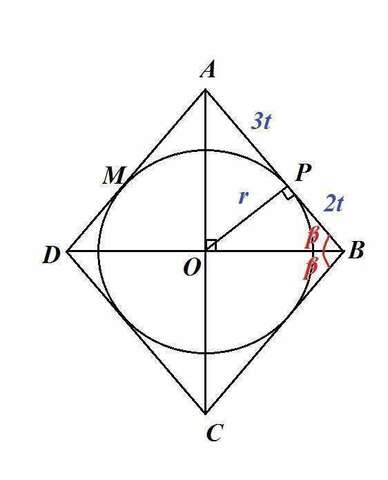
Чертеж к решению задачи во вложении.Обозначим угол $ABC=2\beta$ . Требуется найти синус угла АВС, т.е. $sin2\beta$ .

Пусть t- величина одной части при делении стороны ромба точкой касания окружности. Тогда АР=3t, РВ=2t.

По свойству ромба имеем:

1) BD - биссектриса угла АВС;

2) треугольник АОВ - прямоугольный с углом О=90 градусов.

По свойству касательной к окружности ОР-радиус и ОР перпендикуляен стороне АВ.

По свойству высоты прямоугольного треугольника

$OP^2=AP*PB$ , т.е. $r^2=2t*3t$

Тогда $t=\frac{r}{\sqrt6}$ , $PB=2*\frac{r}{\sqrt6}=\frac{2r}{\sqrt6}$

В прямоугольном треугольнике ОРВ по теореме Пифагора

$OB^2=OP^2+PB^2$

$OB^2 =r^2+(\frac{2r}{\sqrt6})^2=\frac{10r^2}{6}=\frac{5r^2}{3}$

$OB=\frac{r\sqrt5}{\sqrt3}$

$sin2\beta=2sin\beta\ cos\beta$

В теугольнике ОРВ:

$sin\beta=\frac{OP}{OB}=r:\frac{r\sqrt5}{\sqrt3}=\frac{\sqrt3}{\sqrt5}$

$cos\beta=\frac{PB}{OB}=\frac{2r}{\sqrt6} :\frac{r\sqrt5}{\sqrt3}=\frac{2}{\sqrt10}$

Наконец,

$sin ABC=sin2\beta=2*\frac{\sqrt3}{\sqrt5}*\frac{2}{\sqrt10}=\frac{4\sqrt3}{\sqrt50}=\frac{2\sqrt6}{5}$

Ответ: $sin ABC=\frac{2\sqrt6}{5}$

artalex74_zn (25.2k баллов) 12 Март, 18