РЕШЕНИЕ
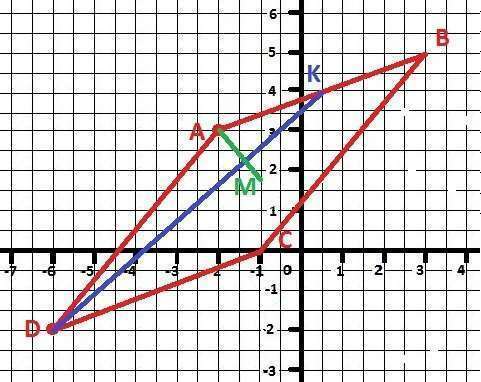
1. Координаты точки В.
Вx = Ax + ABx = -2i+5i = 3i
By = Ay + ABy = 3j + 2j = 5j
B(3,5) - ОТВЕТ
2. Координаты вектора AD
Dx = -6 - (-2) = - 4i
Dy = -2 - 3 = - 5
AD = (-4; -5) - ОТВЕТ
3. Уравнение DC ║ AB.
Коэффициент наклона -k - по вектору АВ.
k = dY/dX = ABj/ABi = 2/5.
Сдвиг прямой - b - по точке D(-6;-2)
Из уравнения прямой - Dy = k*Dx + b
b = Dy - k*Dx = - 2 - 2/5*(-6) = 1/5.
Уравнение прямой CD - Y = 2/5*x + 1/5 или 5Y - 2X = 1 - ОТВЕТ.
4. Координаты точки С из условия AB = CD. Через вектор АВ -
С= D + AB.
Сx = Dx + Bi = -6 + 5 = - 1
Cy = Dy +Bj = - 2 + 2 = 0
Точка С(-1,0) - ОТВЕТ.
5. Угол ADK. Находим координаты точки К - середина АВ.
Kx = (Ax + Bx)/2 = (-2 + 3)/2 = 0.5
Ky = (Ay + By)/2 = (+ 3 + 5)/2 = 4.
Координаты точки К - К(0,5, 4).
Коэффициент наклона прямой АВ
k1 = (Ay-Dy)/(ax-Dx) = (3 - (-2))/(-2 - (-6)) = 5/4
Коэффициент наклона прямой DK.
k2 = 4/6.5 = 8/13
Угол между прямыми по формуле
tg α = (k2 -k1)/(1 + k1*k2) = (5/4 -8/13)/(1 + 10/13) = 33/52 : 1 10/13 = 33/92
α = arctg(0.3587) ~ 0.3444 рад = 19.7° - ОТВЕТ
6) Площадь треугольника ADK
Уравнение прямой DK - Y= x + 3.5
Уравнение высоты AM ⊥ DK - Y = -x+ 5/6
Точка пересечения - М - методом Крамера система уравнений
y+x = 5/6 и y - x = 3 1/2.
Решение - М(-1 1/3, 2 2/7).
Длина высоты АМ - по т. Пифагора = 0,977.
Длина основания DK -= √78.25 = 8.85.
Площадь треугольника ADK
S = DK * AM / 2 = 8.85*0.977/2 ~ 4.326