Чтобы угол между высотами стал равным 150°, они должны выходить из вершины острого угла параллелограмма к продолжениям его сторон.
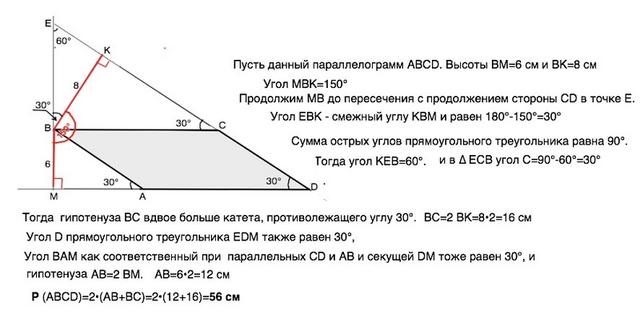
Пусть данный параллелограмм АВСD.
Высоты ВМ=6 см и ВК=8 см
Угол МВК=150°
Продолжим МВ до пересечения с продолжением стороны CD в точке Е.
Угол ЕВК - смежный углу КВМ и равен 180°-150°=30°
Сумма острых углов прямоугольного треугольника равна 90°.
Тогда угол КЕВ=60°.
и в ∆ ЕСВ угол С=90°-60°=30°
Тогда гипотенуза ВС вдвое больше катета, противолежащего углу 30°.
ВС=2 ВК=8•2=16 см
Угол D прямоугольного треугольника ЕDМ также равен 30°,
Угол ВАМ как соответственный при параллельных CD и AB и секущей DM тоже равен 30°, и гипотенуза АВ=2 ВМ.
АВ=6•2=12 см
P (ABCD)=2•(AB+BC)=2•(12+16)=56 см