2)Центр окр-ти, описанной около треуг-ка лежит на пересечении серединных перпендикуляров. То есть из середин сторон восстанавливаются перпендикуляры (достаточно двух) и точка их пересечения будет центром описан. окружности.
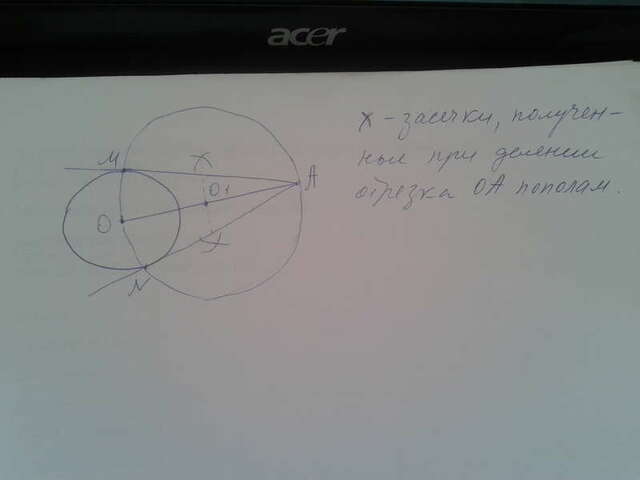
1)Если точка А лежит вне окр-ти, то соединяют её с центром О, делят отрезок АО пополам (тоже с помощью циркуля и линейки), получают точку О_1. Теперь точка О_1 - центр окр-ти с радиусом ,равным АО_1=ОО_1.Окружность с центром О_1 пересечёт заданную окр-ть с центром в точке О в точках M и N. Касательными будут прямые АM и AN, т.к. ОМ и ON перпенд-ны ОА.