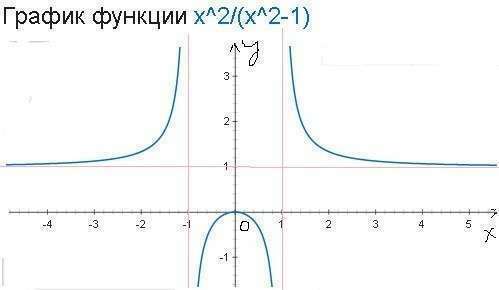
1) ОДЗ, знаменатель ≠1
х²-1≠0, х²≠1, х≠+-1
2) экстремумы
у'=(2x(x²-1)-2x*x²)/(x²-1)²=(2x³-2x-2х³)/(x²-1)²= -2х/(x²-1)²
экстремумы в точках где у'=0 и не существует
х=0, х=+-1
при х<0, y'>0, у возрастает
при х>0, y'<0, y убывает<br>у(0)=0
в точке х=0, у' меняет знак с+ на - ⇒ в точке (0,0) максимум
3) выпуклость вогнутость точки перегиба
у''=( -2(x²-1)+2x*2(x²-1)*2x)/(x²-1)^4=(6x^4-4x²-2)/(x²-1)^4=2(3x^4-2x²-1)/(x²-1)^4
у''=0
x=+-√(2+-√(4+12))/6 , x1=1, x2= -1, х3, х4 - под корнем <0<br>точки х= -1;1 - точки перегиба
при х<-1 и х>1 y''>0 график вогнутый вниз
при х∈(-1;1), y''<0 график выпуклый вверх<br>4) ассимптоты
рассмотрим односторонние пределы
lim x²/(x²-1)=(1/0+)=+∞
х->-1-
lim x²/(x²-1)=(1/0-)= -∞
x->-1+
lim x²/(x²-1)=(1/0-)=-∞
x->1-
lim x²/(x²-1)=(1/0+)=+∞
x->1+
в точках х= - 1 и х=1 бесконечный разрыв, х= -1; х=1 вертикальные ассимптоты
lim x²/(x²-1)=lim1/(1-1/x²)=1 , y=1 горизонтальная ассимптота
x->+-∞