Через внутреннюю точку квадрата, со стороной 12 см, проведены прямые, параллельный его...

Question

Через внутреннюю точку квадрата, со стороной 12 см, проведены прямые, параллельный его сторонам. Одна прямая делит сторону в отношении 1:5, а другая - в отношении 7:5. Образовалось четыре четырёхугольника. Найдите площадь наименьшего четырёхугольника.

Answer 1

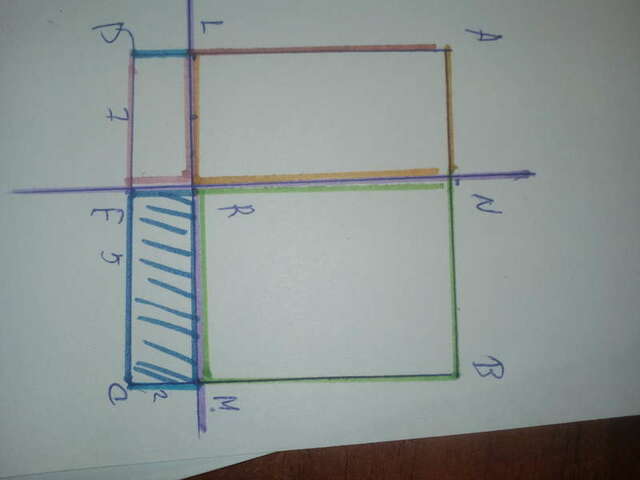
Пусть проведены прямые LM и NE через точку R.
LD:LA = 1:5
AL + LD = AD = 12 см
Тогда AL = 10 см, а , LD = 2 см.
LMCD - прямоугольник => LM = DC = 12 см, LD = MC = 2 см.

DE:EC = 7:5
DE + EC = DC = 12 см
Тогда DE = 7 см, а ЕС = 5 см.
MC < BM, EC < DE. Тогда наименьшую площадь будет иметь прямоугольник REСМ.
SREСМ = EC•MC = 5 см • 2 см = 10 см².
Ответ: 10 см².

---