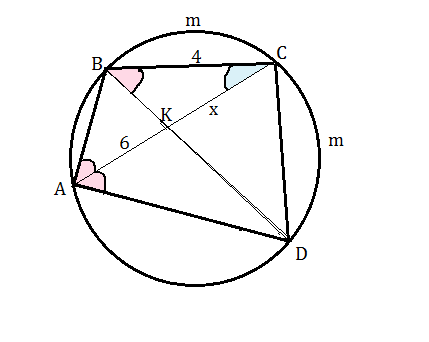
В решении используем свойства вписанных углов и подобных треугольников.
АС - биссектриса.
Равные углы ВАС и САD опираются на равные дуги ВmС и СmD
Но на дугу СmD опирается и угол DВС, следовательно, он равен углу ВАС.
В треугольниках АВС и ВКС имеется общий угол ВСА и равные углы СВК и ВАС Следовательно, они подобны по двум углам.
Из подобия следует
АС:ВС=ВС:КС
ВС²=АС*КС
16=(6+х)*х
х²+6х-16=0
Решив квадратное уравнение, получим два корня: 2 и -8.
Отрицательный корень не подходит.
Следовательно, КС=х=2