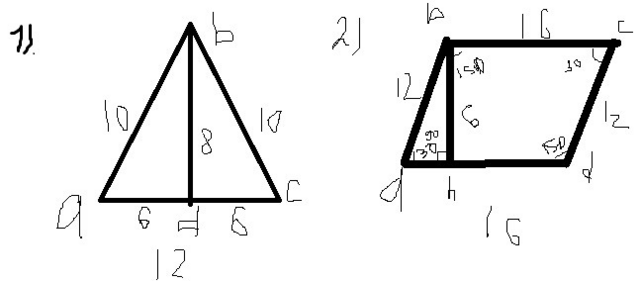
1. Дано: треугольник abc, ab=bc=10см, ac=12см, bd-высота
Т.к. треугольник равнобедренный, следовательно в равнобедренном треугольнике высота является медианой и биссектрисой, а значит ad=dc=12/2=6 см. По теореме Пифагора получим bd=sqrt(bc^2-dc^2)=sqrt(10^2-6^2)=sqrt64=8 (то есть bd=8 см)
Площадь треугольника равна полупроизведению основания на высоту
S=1/2bd*ac=1/2*8*12=48 cм^2
P.S. ^2 - это возведение в степень( то есть например 6^2- это 6 в квадрате или 36)
sqrt - это корень
2. Дано:abcd - параллелограмм, ab=12, bc=16, угол b=150
Решение:Т.к. это параллелограмм, то по свойству противоположные углы равны, следовательно , угол b = углу d = 150. Сумма сторон параллелограмма равна 360, а угол a= углу c , следовательно, уголc a =углу c = (360-150-150)/2=30
Проводим высоту bh. Т.к. высота, то угол ahb=90 градусов, тк катет, лежащий против угла в 30 градусов равен половине гипотенузы, то высота bh=12/2=6.
S=ad*bh=16*6= 96см^2
3.S=1/2(10+20)*12=180 см^2