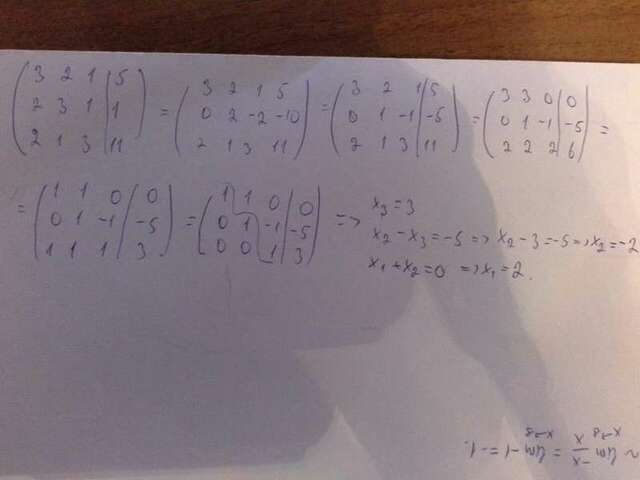Прикрепляю решение СЛАУ, а для проверки совместимости надо проверить что ранг матрицы коэффициэнтов равен рангу расширенной матрицы ( с последним столбцом после знака равно) , то есть две матрицы привести к ступенчатому виду и посмотреть кол-во их ненулевых строк