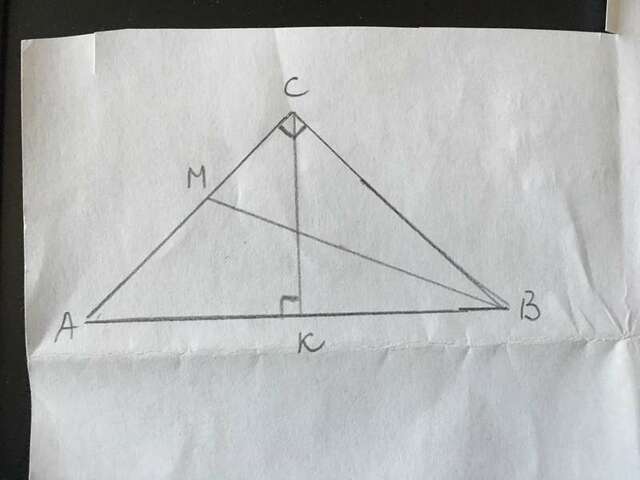
Задача составлена некорректно, но вычислить размер меньшего катета можно.
По условию d=СM=5, h=CK=7, АС - меньший катет и ∠В - меньший из острых.
СК=АС·ВС/АВ ⇒⇒ СК/АС=ВС/АВ.
По теореме биссектрис СМ/АМ=ВС/АВ. Объединим два уравнения:
СК/АС=СМ/АМ,
АС=СК·АМ/СМ=СК·(АС-СМ)/СМ=h(AC-d)/d,
d·АС=h·АС-dh,
AC(h-d)=dh,
AC=dh/(h-d)=5·7/(7-5)=17.5, Не похоже, что это меньший из катетов, ведь высота СК=7, а это намного меньше этого катета. Найдём второй катет.
АМ=АС-СМ=[dh/(h-d)]-d=d²/(h-d),
Опять, по т. биссектрис СМ/АМ=ВС/АВ,
АВ=АМ·ВС/СМ=d·BC/(h-d).
По теореме Пифагора АВ²=АС²+ВС²,
d²·BC²/(h-d)²=[d²h²/(h-d)²]+BC²,
(d²·BC²-BC²(h-d)²)/(h-d)²=d²h²/(h-d)²,
BC²=d²h²/(d²-(h-d)²),
ВС=dh/√(d²-(h-d)²)=5·7/√(5²-(7-5)²)≈7.6,
ВС<АС, значит ВС - меньший из катетов.<br>Ответ: 7.6