1) Область определения- вся числовая ось
2) найдем производную, приравняем к 0, там где производная =0 экстремумы
у'=4x³-4x =0
4x(x²-1)=0
x=-1, x=0, x=1
определим знак производной на интервалах (-∞;-1), (-1;0),(0;1), (1;+∞)
для этого надо взять какое-либо число из каждого интервала например -2; - 0,5; 0,5; 2 подставить в формулу производной и посмотреть какого знака получается значение
при х<-1, y' <0 функция убывает<br>при х∈(-1;0), у'>0, у возрастает
при х∈(0,1), у'<0, y убывает<br>при х>1, y'>0, y возрастает
там где производная меняет знак с - на + минимум а с + на - максимум
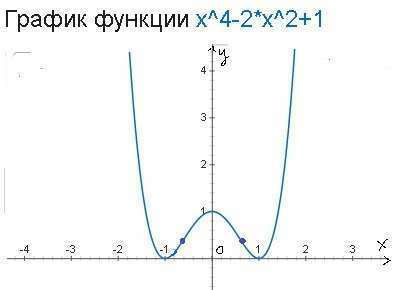
в точках -1 и 1 минимум
в точке 0 максимум
3) у(-x)= y(x) функция четная
4) точки пересечения с осями координат
с осью ОХ у=0
у=x^4-2x²+1=(x²-1)=0, x=+-1
с осью ОУ
х=0, у=1
5) выпуклость вогнутость, точки перегиба
найдем ворую производную и приравняем ее к 0
у''=12x²-4=0
4(3x²-1)=0
3x²-1=0
x²=1/3
x=+-∛(1/3)≈+-0,7 - точки перегиба графика
определим знак второй производной на интервалах
(-∞;-∛(1/3)) , (-∛(1/3);∛(1/3)) , (∛(1/3);+∞)
для этого надо взять какие-либо значения х из этих интервалов например -2; 0 ;2 подставить в формулу второй производной и посмотреть какой знак получается
на интервале (-∞;-∛(1/3)) и на интервале (∛(1/3)) y''>0 на этих интервалах график вогнут вниз
(-∛(1.3); ∛(1/3)) у''<0 на этом интервале график выпуклый вверх<br>