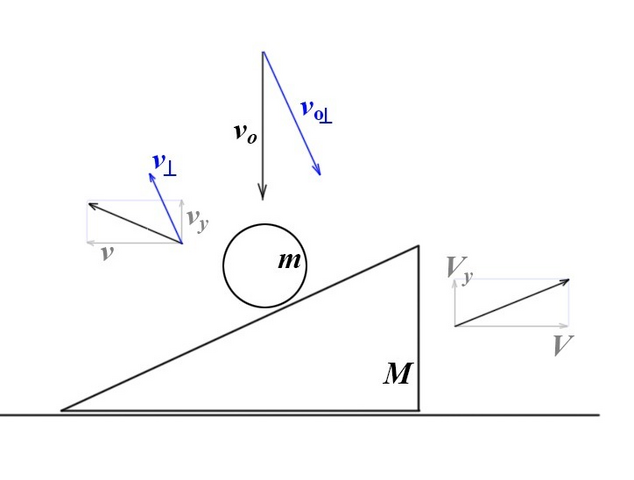
По окончании взаимодействия у клина и шара будут какие-то неизвестные нам пока что скорости 
и 
(вдоль стены – без индексов, поперёк стены – с индексом). Как векторы – эти два искомых вектора представляют собой набор четырёх неизвестных. Но для взаимодействия сразу трёх тел мы можем составить систему только трёх уравнений:
1-ое:
Закон Сохранения составляющей Импульса шара, продольной к клину.
2-ое: Закон Сохранения Импульса вдоль стены.
3-ье: Закон Сохранения Энергии.
Решая такую систему – мы не сможем найти неизвестные. При любой попытке такого решения они будут, так или иначе, взаимозависимы.
Но в задаче и не требуется находить точное значение продольной к стене составляющей конечной скорости клина, а спрашивается лишь о диапазоне возможных значений этой скорости.
В чём же проблема несоответствия числа переменных и уравнений? Всё дело в том, что при взаимодействии сразу трёх тел, в самом деле, возможны разные исходы, результатирующие скорости которых зависят от соотношения упругих свойств взаимодействующих тел. И, разумеется, в любом случае – результатирующие скорости будет строго соответствовать трём приведённым выше уравнениям, но самих решений может быть бесконечно много. И всё что мы можем тут узнать – диапазон этих решений.
Взаимодействие шара с клином и клина со стеной можно в первом приближении рассматривать, как упругое взаимодействие. Правда, такое взаимодействие не обязательно будет описываться линейным Законом Гука. Степень многочлена 
корректно описывающего такое упругое взаимодействия может быть и больше единицы, особенно это касается взаимодействия шара и клина. Как бы то ни было, логично считать, что законы этих упругих взаимодействий – суть монотонно возрастающие (в допустимых для нас пределах) по модулю функции от величины поперечного сжатия.
Если бы мы для уточнения решения стали бы вводить такие конкретные функции, то мы бы столкнулись с двумя проблемами. Во-первых: таких функций – бесконечно много, а во-вторых: мы бы получали очень сложные дифференциальные уравнения, с решениями возможно даже не гармонической природы. Так что такой подход нам не поможет.
Подойдём с другой стороны. Рассмотрим предельные случаи.
Предельный случай [[[ K >>> k ]]]
Допустим, что упругое взаимодействие клина и стены (но не шара и клина!), как функция от величины ненулевого сжатия – стремится к бесконечности, т.е. линейный член 
Тогда если бы клин имел ненулевые смещения поперёк стены, то сила упругости была бы бесконечной. Так что всё ненулевое время взаимодействия шара и клина, клин будет оставаться неподвижным в поперечном к стене направлении, т.е. в том же самом поперечном положении – вплотную, как и изначально, автоматически уравновешивая воздействие шара за счёт бесконечной упругости взаимодействия со стеной. Поскольку клин относительно стены неподвижен – то и его финальная поперечная к стене скорость равна нулю. А это означает, что одну из неизвестных в указанных выше уравнениях мы уже знаем: 
Решим исходя из этого – приведённую выше систему, введя понятие поперечной и продольной к клину скорости шара 
и 
Продольная скорость шара 
измениться не может, так что мы её и не будем учитывать в энергетическом уравнении.
Вдоль стены получаем ЗСИ: 
Составим энергетическое уравнение:
Предельный случай [[[ K <<< k ]]]<br>
Допустим, что упругое взаимодействие клина и шара (но не клина и стены!), как функция от величины ненулевого сжатия – стремится к бесконечности, т.е. линейный член 
Тогда за нулевое время
( 
) удара шара о клин – взаимодействие клина и стены даже не успеет начаться. В таком случае нам даже не нужно рассматривать взаимодействие сразу трёх тел, а достаточно рассмотреть мгновенное взаимодействие шара и клина, а затем уже клина и стены. Т.е. у нас появляется ещё одно уравнение, закон сохранения импульса по нормали к стене. И система опять же решается.
ПРОДОЛЖЕНИЕ В ПРИЛОЖЕНИИ : : :
