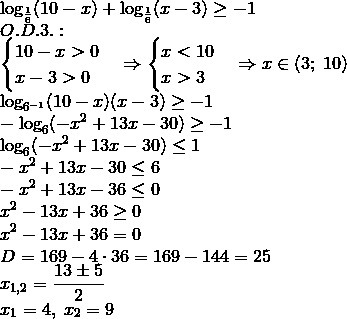0\\x-3>0\end{cases}\Rightarrow\begin{cases}x<10\\x>3\end{cases}\Rightarrow x\in(3;\;10)\\\log_{6^{-1}}(10-x)(x-3)\geq-1\\-\log_6(-x^2+13x-30)\geq-1\\\log_6(-x^2+13x-30)\leq1\\-x^2+13x-30\leq6\\-x^2+13x-36\leq0\\x^2-13x+36\geq0\\x^2-13x+36=0\\D=169-4\cdot36=169-144=25\\x_{1,2}=\frac{13\pm5}2\\x_1=4,\;x_2=9" alt="\log_{\frac16}(10-x)+\log_{\frac16}(x-3)\geq-1\\O.D.3.:\\\begin{cases}10-x>0\\x-3>0\end{cases}\Rightarrow\begin{cases}x<10\\x>3\end{cases}\Rightarrow x\in(3;\;10)\\\log_{6^{-1}}(10-x)(x-3)\geq-1\\-\log_6(-x^2+13x-30)\geq-1\\\log_6(-x^2+13x-30)\leq1\\-x^2+13x-30\leq6\\-x^2+13x-36\leq0\\x^2-13x+36\geq0\\x^2-13x+36=0\\D=169-4\cdot36=169-144=25\\x_{1,2}=\frac{13\pm5}2\\x_1=4,\;x_2=9" align="absmiddle" class="latex-formula">