1.
Площадь параллелограмма (S) = h x основание.
Известно, h=9см, S=108, т. е. основание = 108:9= 12см. (одна сторона)
Далее.
Высота вместе с основанием и косой стороной образуют ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК. В котором катеты = 9 и 12. По т-ме Пифагора гипотенуза этого треуг. (вторая сторона) = Корень квадратный из (9*9 +12*12) = 15 .
2.
Дано:
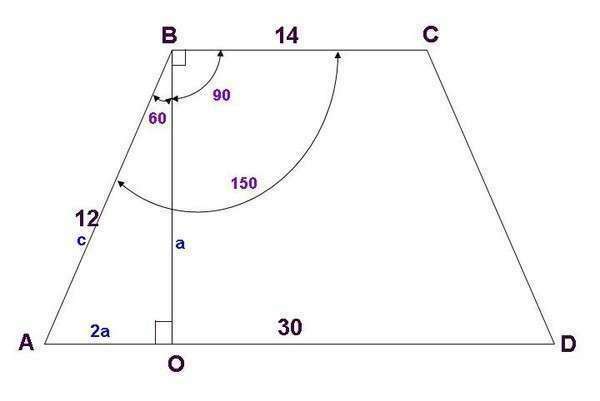
АВ=12, ВС=14, АD=30. угол АВС=150.
Найти: Sавсd-?
Sabcs = 1/2(BC+AD) *BO = 1/2(14+30)*ВО=22*ВО. Осталось найти ВО.
В прямоугольном треугольнике АВО (где ВО=h трапеции) , угол В = 60 (150 - 90).
Известно, что в прямоуг. треуг. отношение противолежащ. катета к прилежащ. = tg угла. = tg60 = 2, т. е. ВО=1/2 АО.
Пусть BO=а, тогда по т-ме ПИФАГОРА
12х12 = (2а) (2а) + а*а
144=5 а*а,
а*а=144:5=28,8; a ~5,366