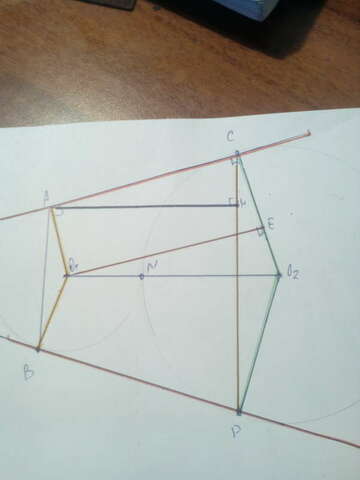
Дано:
ω(O1; R1)
ω(O2; R2)
ω(О1;R1)∩ω(O2;R2) = N
AC, BD - общие касательные
A∈ω (O1;R1)
B∈ω(O1; R1)
C∈ω (O2;R2)
D∈ω(O2; R2)
R1 = 12
R2 = 20
AH⊥CD
---------------------
AH - ?
Решение:
Пусть O1E⊥CO2. Тогда AO1CE - прямоугольник, т.к. ∠O1AC = ∠ACO1 = ∠O1EC = 90°.
Тогда AC = O1E - как противоположные стороны прямоугольника.
O1O2 = R1 + R2.
CE = AO1 - опять же, .к. AO1EC - прямоугольник. Тогда CE = R2 - AO1 = R2 - R1.
По теореме Пифагора в ∆O1EC:
O1E = √O1O2² - EO2² = √(R1 + R2)² - (R2 - R1)² = √R1² + 2R1R2 + R2² - R2² + 2R1R2 - R1² = √4R1R2 = 2√R1R2.
∠ACH =1/2UCD - как угол между касательной и хордой.
∠O1O2C = UNC = 1/2UCD (т.к. UNC = UND) - как центральный угол.
Тогда ∠O1O2C = ∠ACD => sinACD = sinO1O2C.
sinO1O2C = O1E/O1O2 = 2√R1R2/(R1 + R2) => sinACD = 2√R1R2/(R1 + R2).
sinACD = AH/AC => AH = sinACD•AC = 2√R1R2•2√R1R2/(R1 + R2) = 4R1R2/(R1 + R2)
Подставляем значения R1 и R2:
AH = 4•12•20/(12 + 20) = 960/32= 30.
Ответ: 30.