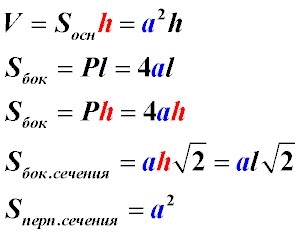Правильная четырехугольная призма
Определение.
Правильная четырехугольная призма - это шестигранник, основаниями которого являются два равных квадрата, а боковые грани представляют собой равные прямоугольники
Боковое ребро - это общая сторона двух смежных боковых граней
Высота призмы - это отрезок, перпендикулярный основаниям призмы
Диагональ призмы - отрезок, соединяющий две вершины оснований, которые не принадлежат к одной грани
Диагональная плоскость - плоскость, которая проходит через диагональ призмы и ее боковые ребра
Диагональное сечение - границы пересечения призмы и диагональной плоскости. Диагональное сечение правильной четырехугольной призмы представляет собой прямоугольник
Перпендикулярное сечение (ортогональное сечение) - это пересечение призмы и плоскости, проведенной перпендикулярно ее боковым ребрам
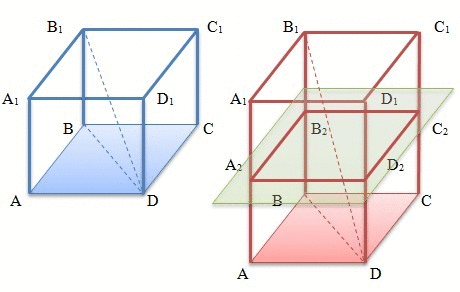
Элементы правильной четырехугольной призмы
Рис.1
На рисунке изображены две правильные четырехугольные призмы, у которых обозначены соответствующими буквами:
Основания ABCD и A1B1C1D1 равны и параллельны друг другу
Боковые грани AA1D1D, AA1B1B, BB1C1C и CC1D1D, каждая из которых является прямоугольником
Боковая поверхность - сумма площадей всех боковых граней призмы
Полная поверхность - сумма площадей всех оснований и боковых граней (сумма площади боковой поверхности и оснований)
Боковые ребра AA1, BB1, CC1 и DD1.
Диагональ B1D
Диагональ основания BD
Диагональное сечение BB1D1D
Перпендикулярное сечение A2B2C2D2 .
Свойства правильной четырехугольной призмы
Основаниями являются два равных квадрата
Основания параллельны друг другу
Боковыми гранями являются прямоугольники
Боковые грани равны между собой
Боковые грани перпендикулярны основаниям
Боковые ребра параллельны между собой и равны
Перпендикулярное сечение перпендикулярно всем боковым ребрам и параллельно основаниям
Углы перпендикулярного сечения - прямые
Диагональное сечение правильной четырехугольной призмы представляет собой прямоугольник
Перпендикулярное (ортогональное сечение) параллельно основаниям
Формулы для правильной четырехугольной призмы
Рис.2
Указания к решению задач
При решении задач на тему "правильная четырехугольная призма" подразумевается, что:
Правильная призма — призма в основании которой лежит правильный многоугольник, а боковые ребра перпендикулярны плоскостям основания. То есть правильная четырехугольная призма содержит в своем основании квадрат. (см. выше свойства правильной четырехугольной призмы)
Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ .
Задача.
В правильной четырёхугольной призме площадь основания 144 см2, а высота 14 см. Найти диагональ призмы и площадь полной поверхности.
Решение.
Правильный четырехугольник - это квадрат.
Соответственно, сторона основания будет равна √144 = 12 см.
Откуда диагональ основания правильной прямоугольной призмы будет равна
√( 122 + 122 ) = √288 = 12√2
Диагональ правильной призмы образует с диагональю основания и высотой призмы прямоугольный треугольник. Соответственно, по теореме Пифагора диагональ заданной правильной четырехугольной призмы будет равна:
√( ( 12√2 )2 + 142 ) = 22 см
Ответ: 22 см
Задача
Определите полную поверхность правильной четырехугольной призмы, если ее диагональ равна 5 см, а диагональ боковой грани равна 4 см.
Решение.
Поскольку в основании правильной четырехугольной призмы лежит квадрат, то сторону основания (обозначим как a) найдем по теореме Пифагора:
a2 + a2 = 52
2a2 = 25
a = √12,5
Высота боковой грани (обозначим как h) тогда будет равна:
h2 + 12,5 = 42
h2 + 12,5 = 16
h2 = 3,5
h = √3,5
Площадь полной поверхности будет равна сумме площади боковой поверхности и удвоенной площади основания
S = 2a2 + 4ah
S = 25 + 4√12,5 * √3,5
S = 25 + 4√43,75
S = 25 + 4√(175/4)
S = 25 + 4√(7*25/4)
S = 25 + 10√7 ≈ 51,46 см2 .
Ответ: 25 + 10√7 ≈ 51,46 см2 .
15306.1214
h2 = 3,5
h = √3,5
Площадь полной поверхности будет равна сумме площади боковой поверхности и удвоенной площади основания
S = 2a2 + 4ah
S = 25 + 4√12,5 * √3,5
S = 25 + 4√43,75
S = 25 + 4√(175/4)
S = 25 + 4√(7*25/4)
S = 25 + 10√7 ≈ 51,46 см2 .
Ответ: 25 + 10√7 ≈ 51,46 см2 .
15306.1214 ш