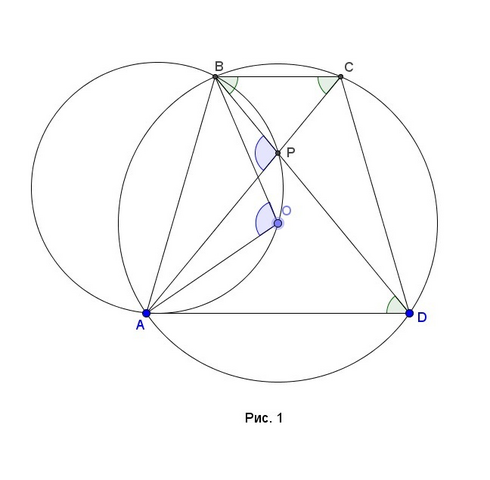
3. ∠BOA=2∠ADB т.к. ∠ADB - вписанный угол, а ∠AOB - центральный. ∠APB=∠PBC+∠PCB=2∠ADB, т.к. ∠APB - внешний угол треугольника PBC и ∠PBC=∠PCB=∠ADB в силу равнобедренности трапеции. Значит, ∠BOA=∠АPВ, т.е. ABPO - вписанный 4-угольник. (см. рис. 1).
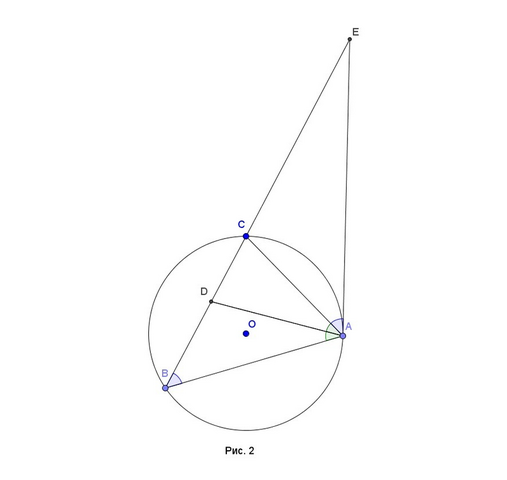
4. Без ограничения общности можно считать, что С лежит между B и Е. Тогда ∠B=∠CAE, т.к. ∠B - вписанный, а ∠CAE - угол между касательной и хордой в точку касания (см. рис 2). ∠EDA=∠B+∠BAD как внешний угол треугольника BAD. ∠EAD=∠CAE+∠CAD, но ∠BAD=∠CAD (AD - биссектриса). Значит ∠EDA=∠EAD, т.е. EAD - равнобедренный и AE=ED.