|х+2|-|2х+8|=а;
Это уравнение можно решить методом интервалов.
Находим нули модулей:
х+2=0;
х=-2;
2х+8=0;
2х=-8;
х=-4.
Получаем интервалы:
(-∞;-4), [-4;-2), [-2;+∞).
На этих интервалах модули имеют следующие знаки:
(х+2): - - +
(2х+8): - + +
Раскрываем модули в соответствии со знаками:
1) -x-2+2x+8=a;
a=x+6.
2) -x-2-2x-8=a;
a=-3x-10.
3) x+2-2x-8=a;
a=-x-6.
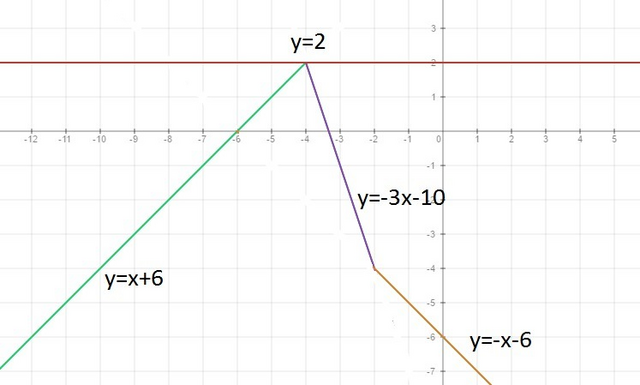
Теперь построим графики функций, приняв а=у:
у=х+6 на отрезке (-∞;-4);
у=-3х-10 на отрезке [-4;-2);
y=-x-6 на отрезке [-2;+∞).
На графике хорошо видно, что одно решение это уравнение имеет при а=у=2.
Ответ: 2.