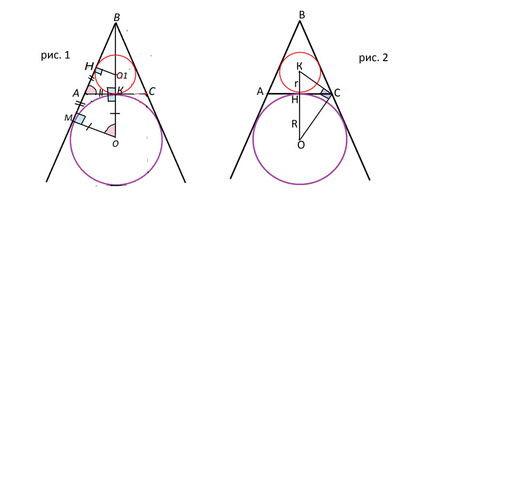
Решений у этой задачи несколько - есть посложнее и подлиннее есть попроще и покороче.
Во вложении даны два рисунка. Один для любителей более сложных решений через подобие четырехугольников НАКО1 и КОМА в рис. 1
Более простое решение, к нему дан рисунок 2
Соединим центры окружностей - вписанной в треугольник АВС и вневписанной.
Точку С также соединим с этими центрами.
Угол КСО прямой, т.к. равен сумме половин смежных углов ( центры окружностей лежат на биссектрисах углов).
Треугольник КСО - прямоугольный.
СН в нем -высота и равна половине АС, т.е. равна 5 см
Отрезок ОН равен радиусу вневписанной окружности и равен 7,5
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится
гипотенуза этой высотой.
Из этого следует равенство:
СН²=ОН·КН
25=7,5КН
r =КН=25:7,5=3 ¹⁄₃