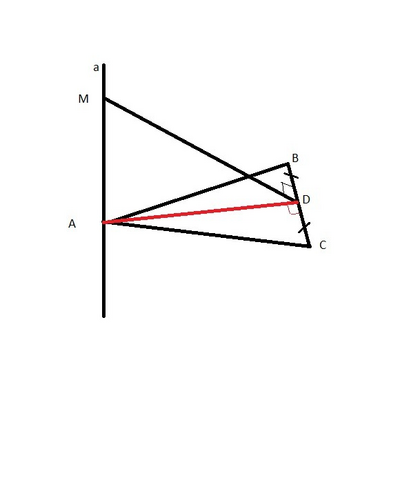
Дано:
a⊥ABC
MD⊥BC
BD = DC
Решение:
1) т.к. a⊥ABC, то a ⊥ любой прямой лежащей в этой плоскость ⇒ a⊥BC
2)
Соединим A и D.
a и MD находятся в одной плоскости и пересекаются
BC⊥a ( доказано в действии 1), BC⊥MD по условию ⇒ BC ⊥ двум пересекающимся прямым в плоскости ⇒ BC ⊥ плоскости MAD ⇒ BC ⊥ любой прямой лежащей в этой плоскости ⇒ BC ⊥ AD
3) т.к. BD = DC ⇒ AD - медиана. AD ⊥ BC (из действия 2) ⇒ AD - высота.
т.к. AD и медиана и высота ⇒ ΔABC - равнобедренный ⇒ AB = AC
или
3) AD⊥BC (из действия 2) ⇒ ΔABD и ΔACD - прямоугольные
обозначим AD = h, BD = DC = a
по т. Пифагора
AB² = h² + a²
AC² = h² + a²
h² + a² = h² + a²
⇒
AB² = AC²
AB = AC
или
3)
через tg/ctg