В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и...

Question

В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45 градусам. Найдите площадь трапеции.

Answer 1

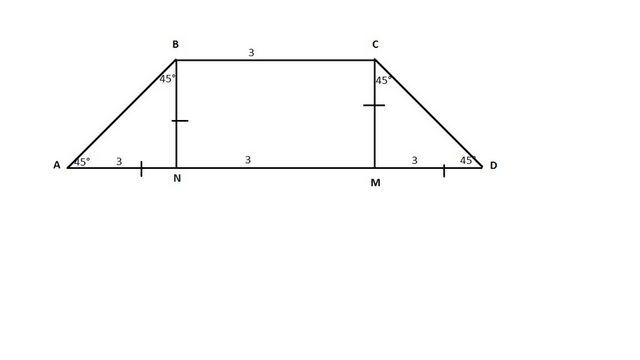
Проведём две высоты BN и CM.
Т.к. ∠BAN = 45°, то ΔBAN - равнобедренный ⇒ BN = AN.
Рассмотрим ΔBAN и ΔCDM.
∠BAN = ∠CDM - по условию.
BN = CM, т.е. BCMN - прямоугольник.
∠BNA = ∠CMD = 90°
Значит, ΔBAN = ΔCDM - по катету и острому углу.
Тогда AN = MD.
BC = NM, т.к. BCMN - прямоугольник ⇒ MN = 3.
AN + MD = AD - NM = 9 - 3 = 6 ⇒ AN = MD = 3.
Тогда и BN = 3.

Ответ: 18.

---