Пожалуйста помогите..........................................

Question

Пожалуйста помогите..........................................

---

Answer 1

1. Обозначим за R радиус описанной окружности, за r - вписанной.
Известно, что радиусы вписанной и описанной окружности около правильного многоугольника связаны формулой:
r = R•cos(180°/n), где n - количество сторон.
Отсюда cos(180°/n) = r/R.
cos(180°/n) = 5 см/10 см
cos(180°/n) = 1/2
arccos(1/2) = 60°.
180°:60° = 3.
Ответ: 3 стороны.

2.Известно, что около любого правильного многоугольника можно описать окружность. Опишем окружность.
KE и MN - хорды этой окружности. По теореме о произведении хорд окружности:
MF•FN = KF•FE
6•8 = KF(16 - KF)
-KF² + 16KF = 48
KF² - 16KF + 48 = 0

KF1 + KF2 = 16
KF1•KF2 = 48

KF1 = 12
KF2 = 4

KF = 12
FE = 4

KF = 4
FE = 12
Ответ: 4 см; 12 см.

Answer 2

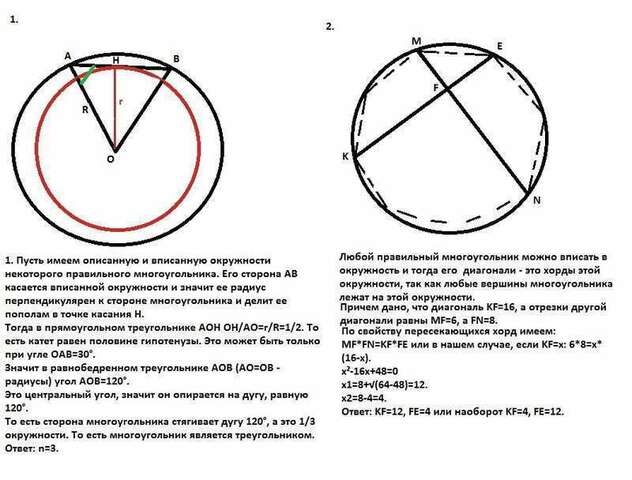
1. Пусть имеем описанную и вписанную окружности некоторого правильного многоугольника. Его сторона АВ касается вписанной окружности и значит ее радиус перпендикулярен к стороне многоугольника и делит ее пополам в точке касания Н.
Тогда в прямоугольном треугольнике АОН ОН/АО=r/R=1/2. То есть катет равен половине гипотенузы. Это может быть только при угле ОАВ=30°.
Значит в равнобедренном треугольнике АОВ (АО=ОВ - радиусы) угол АОВ=120°.
Это центральный угол, значит он опирается на дугу, равную 120°.
То есть сторона многоугольника стягивает дугу 120°, а это 1/3 окружности. То есть многоугольник является треугольником.
Ответ: n=3.

2. Любой правильный многоугольник можно вписать в окружность и тогда его  диагонали - это хорды этой окружности. По свойству пересекающихся хорд имеем:
MF*FN=KF*FE или в нашем случае, если KF=x: 6*8=х*(16-х).
х²-16х+48=0
х1=8+√(64-48)=12.
х2=8-4=4.
Ответ: KF=12, FE=4 или наоборот KF=4, FE=12.

---