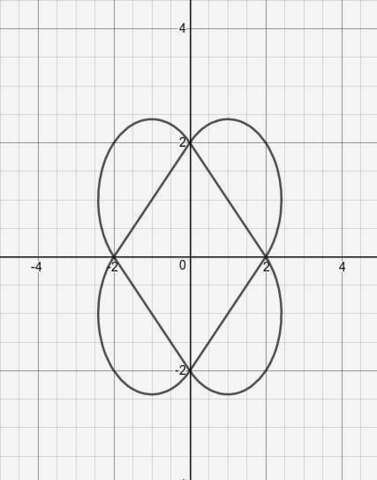
(x²+y²-2|x|-2|y|)(|x|+|y|-2)=0
уравнение распадается на 2 независимые части x²+y²-2|x|-2|y|=0 и |x|+|y|-2=0
рассмотрим уравнение разбив плоскость на тригонометрческие четверти.
1) x≥0, y≥0
|x|=x, |y|=y
x²+y²-2x-2y=0 и x+y-2=0
x²+y²-2x-2y=(x²-2x+1)+(y²-2y+1)-2=(x-1)²+(y-1)²-2=0
(x-1)²+(y-1)²=2 - это окружность с цетром в точке (1;1) и радиусом √2
x+y-2=0
y=-x+2 прямая, проходящая через точки (0;2) и (2;0)
2) x<0, y≥0<br>|x|=-x, |y|=y
x²+y²+2x-2y=0 и -x+y-2=0
x²+y²+2x-2y=(x²+2x+1)+(y²-2y+1)-2=(x+1)²+(y-1)²-2=0
(x+1)²+(y-1)²=2 - это окружность с цетром в точке (-1;1) и радиусом √2
-x+y-2=0
y=x-2 прямая, проходящая через точки (0;2) и (-2;0)
3) x<0, y<0<br>|x|=-x, |y|=-y
x²+y²+2x+2y=0 и -x-y-2=0
x²+y²+2x+2y=(x²+2x+1)+(y²+2y+1)-2=(x+1)²+(y+1)²-2=0
(x+1)²+(y+1)²=2 - это окружность с цетром в точке (-1;-1) и радиусом √2
-x-y-2=0
y=-x-2 прямая, проходящая через точки (-2;0) и (0;-2)
4) x≥0, y<0<br>|x|=x, |y|=-y
x²+y²-2x+2y=0 и -x-y-2=0
x²+y²-2x+2y=(x²-2x+1)+(y²+2y+1)-2=(x-1)²+(y+1)²-2=0
(x-1)²+(y+1)²=2 - это окружность с цетром в точке (1;-1) и радиусом √2
x-y-2=0
y=x-2 прямая, проходящая через точки (0;-2) и (2;0)
Рисуем. На картинке исказились пропорции, дожны быть окружности, а не овалы.