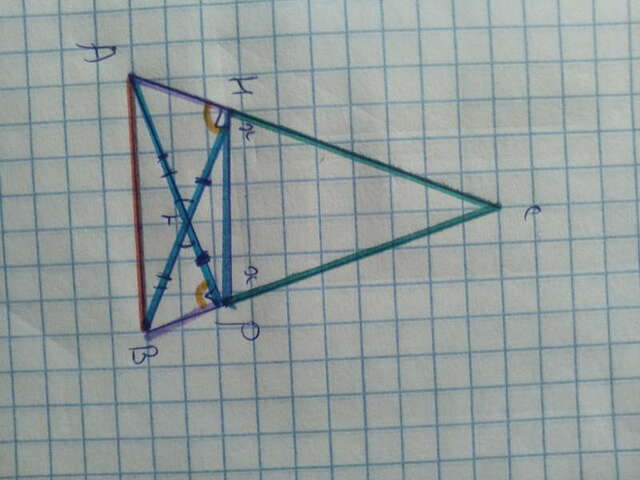Рассмотрим ∆CHP.
CH = PC => ∆CHP - равнобедренный. Значит, ∠CPH = ∠CHP - как углы при основании.
Обозначим ∠CPH за x. Тогда ∠PHL = 90° - x (т.к. ∠LHC = 90°).
∠LPH = 90° - ∠CHP = 90° - x
(L - точка пересечения высот).
Тогда ∠LPH = ∠LHP => ∆LHP - равнобедренный. Тогда LH = LP.
∠BPA = 90° + ∠LPH = 180° - x.
∠BHA = 90° + ∠LHP = 180° - x.
Тогда ∠BPA = ∠BHA.
Рассмотрим ∆ALH и ∆BLP.
PL = LH
∠BPL = ∠AHL
∠BLP = ∠AH - как вертикальные.
Значит, ∆BLP = ∆ALH - по II признаку.
Из равенства треугольников => BL = LA.
BH = BL + LH
AP = AL + LP
LP = LH
Значит, BH = AP.