По углу правильного многоугольника можно найти количество сторон:
α(n)=(n-2)*180°/n;
135°=(n-2)*180°/n;
180°n-360=135n;
180°n-135°n=360;
45°n=360°;
n=8.
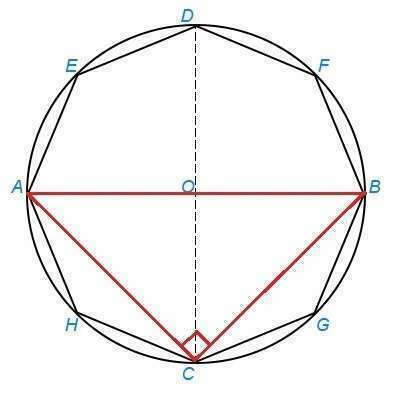
Таким образом, фигура - восьмиугольник. Если восьмиугольник вписать в окружность, получаем, что большая диагональ равна диаметру окружности, или гипотенузе АВ прямоугольного треугольника АВС, а меньшие диагонали равные катеты АС=ВС=21√2.
АВ можно найти по т.Пифагора АВ=√(АС²+ВС²)=√(882+882)=√1764=42.
Можно найти АВ проще. Рассмотреть АВ как диагональ квадрата, тогда АВ=АС√2=21√2*√2=21*2=42.
Ответ: 42.