№1.
а)
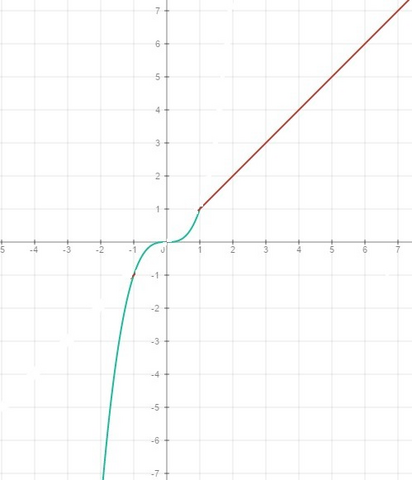
f(x)=x³, если х≤1, - зеленый график
f(x)=x, если х>1. - красный график
Свойства:
1) D=R;
2) E=R;
3) Наибольшего и наименьшего значений не имеет;
4) Точка пересечения с осями координат: (0;0);
5) Нули функции: х=0;
6) При х≤1 y≤0, при x>1 y>0;
7) Ни четная, ни нечетная;
8) Нарастает на R;
9) Не периодическая.
в)
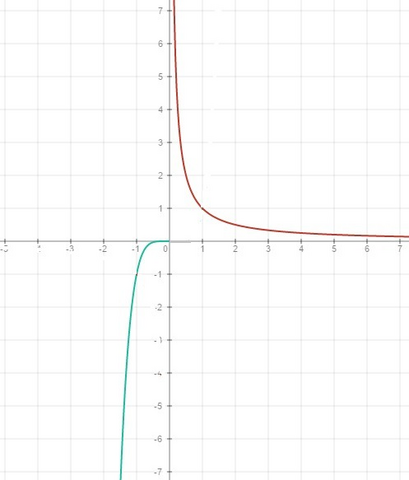
f(x)=x^5, если х≤0, - зеленый график
f(x)=1/x, если х>0. - красный график
Свойства:
1) D=(-∞;0]∪(0; +∞);
2) E=(-∞;0]∪(0;+∞);
3) Наибольшего и наименьшего значений не имеет;
4) Точка пересечения с осями координат: (0;0) - для графика y=x^5;
5) Нули функции: х=0 - для графика y=x^5;
6) При х≤0 у≤0, при х>0 y>0;
7) Ни четная, ни нечетная;
8) Нарастает на (-∞;0), спадает на (0;+∞)
9) Не периодическая.
№2.





4x-3≠0;
4x≠3;
x≠3/4.
На промежутке (-∞;3/4) значения отрицательные, на промежутке (3/4;+∞) значения положительные.
Ответ: (3/4;+∞).