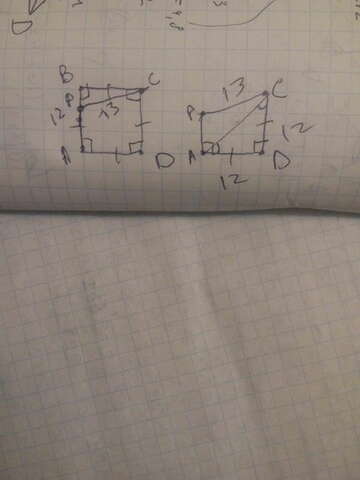
Слева полный чертёж, справа используемая часть для наглядности.
Рассмотрим два треугольника: ∆АDC и ∆APC
найдём АС в прямоугольном треугольнике АСD:
АС²=АD²+CD²=12²+12²=144+144=288
АС=√288=12√2≈16.97
Sтреуг=1/2*AD*DC=1/2*12*12=72см²
---
теперь треугольник АРС
РА найдём через косинус
косинус угла РАС называется отношение прилежащего катета к гипотенузе:
cos(PAC)=PA/РС
диагонали квадрата делят его углы на две равных части, слодовательно угол РАС=90/2=45°
cos(45°)=РА/13
√2/2=РА/13
находим через пропорцию; РА=х
√2/2=х/13
13√2=2х
х=(13√2)/2≈9.19
РА=(13√2)/2
через две стороны и угол считаем площадь второго треугольника:
S∆=1/2*РА*АС*sin(PAC)
S∆=1/2*(13√2)/2*12√2*sin45
S∆=3√2*13√2*√2/2= 3*2*13*√2/2= 3*13*√2=39√2≈55.154 (см²)
___
теперь складываем площади этих двух фигур:
72+39√2≈127.154 см²
Ответ: S=127.154 см²