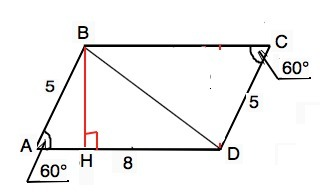
Сумма двух углов 120°, значит, острые углы равны по 60°.
По т.косинусов
BD=√(AB²+AD²-2AB•AD•cos60°)=√(64+25-80/2)=7 ед. длины.
Или
Опустим из В на АD высоту ВН.
ВН=AB•sin60°=2,5√3
AH=АВ•cos60°=2,5--
HD=8-2,5=5,5
По т.Пифагора
ВD=√(BH²+DH²)=√(18,25+30,24)=7 ед.длины.