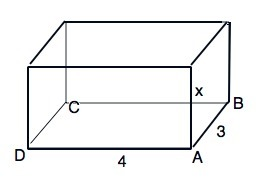
Площадь поверхности прямоугольного параллелепипеда состоит из площади двух оснований и площади боковой поверхности.
Пусть 3 и 4 - ребра оснований, выходящие из вершины А, а х - длина бокового ребра из той же вершины А.
Тогда 2Ѕ (осн)=2•3•4=24 (ед. площади)
Площадь боковой поверхности прямоугольного параллелепипеда равна произведению длины бокового ребра на периметр основания.
Ѕ(бок)=х•2(3+4)=14х
Ѕ(полн)=14х+24=52
. 14х=28
х=28:14=2 (ед. длины)
Третье ребро равно 2 (ед длины)