Найти площадь криволинейной трапеции, ограниченной следующими графиками: y = 2x; y = x^2....

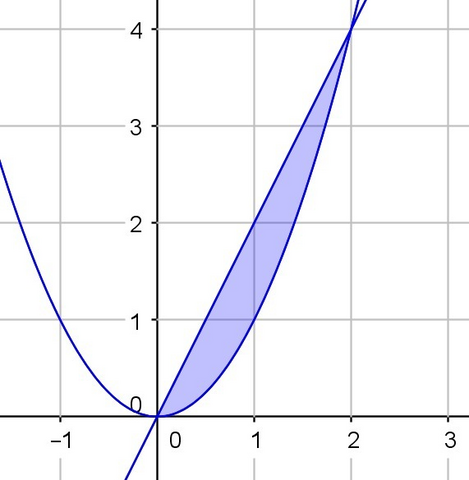
Область имеет вид, изображённый на рисунке. Точки пересечения графиков находим из решения системы
{y = 2x, y = x^2}
(x, y) = (0, 0) или (2, 4)

Площадь подграфика равна определённому интегралу от функции, площадь такой криволинейной трапеции - от разности функций.

$S=\int_0^2(2x-x^2)\,dx=\left.x^2-\frac{x^3}3\right|_0^2=4-\frac83-0=\frac43$

Ответ. S = 4/3